Question

16．对于正数x，用符号[x]表示x的整数部分，例如：[0.1]=0，[2.5]=2，[3]=3．点A（a，b）在第一象限内，以A为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直．其中垂直于y轴的边长为a，垂直于x轴的边长为[b]+1，那么，把这个矩形覆盖的区域叫做点A的矩形域．例如：点$（3，\frac{3}{2}）$的矩形域是一个以$（3，\frac{3}{2}）$为对角线交点，长为3，宽为2的矩形所覆盖的区域，如图1所示，它的面积是6．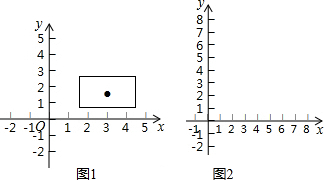

根据上面的定义，回答下列问题：
（1）在图2所示的坐标系中画出点$（2，\frac{7}{2}）$的矩形域，该矩形域的面积是8；
（2）点$P（2，\frac{7}{2}），Q（a，\frac{7}{2}）（a＞0）$的矩形域重叠部分面积为1，求a的值；
（3）已知点B（m，n）（m＞0）在直线y=x+1上，且点B的矩形域的面积S满足4＜S＜5，那么m的取值范围是$\frac{4}{3}$＜m＜$\frac{5}{3}$．（直接写出结果）

Answer 1

分析 （1）点（2，$\frac{7}{2}$）的矩形域的定义，求出矩形边长分别为2，4，画出图形即可解决问题；
（2）分两种情形，重叠部分在（1）中矩形的左边或右边，分别构建方程即可解决问题；
（3）利用特殊值法．推出平行于y轴的矩形的边长为3，由此即可解决问题；

解答 解：（1）点（2，$\frac{7}{2}$）的矩形域如图所示：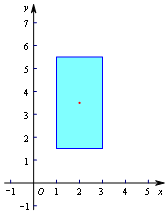

该该矩形域的面积是8．

（2）如图所示，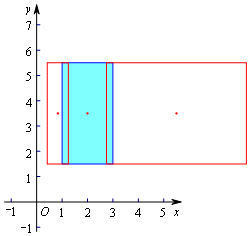

因为点P（2，$\frac{7}{2}$），Q（a，$\frac{7}{2}$）（a＞0）的矩形域重叠部分面积为1，且平行于y轴的边长均为4，
所以点点P（2，$\frac{7}{2}$），Q（a，$\frac{7}{2}$）（a＞0）的矩形域重叠部分也是一个矩形，且平行于y轴的边长为4，平行于x轴的边长为$\frac{1}{4}$．
①当0＜a＜2时，a+$\frac{a}{2}$=1+$\frac{1}{4}$，解得a=$\frac{5}{6}$；

②当a＞2时，a-$\frac{a}{2}$=3-$\frac{1}{4}$，解得a=$\frac{11}{2}$．
所以a的值为$\frac{5}{6}$或$\frac{11}{2}$．
   
（3）当m=1时，S=2，
当m=2时，S=6，
∵4＜S＜5，
∴1＜m＜2，
∴平行于y轴的矩形的边长为3，
∴平行于x轴的矩形的边长m的范围为$\frac{4}{3}$＜m＜$\frac{5}{3}$．
故答案为$\frac{4}{3}$＜m＜$\frac{5}{3}$．

点评 本题考查一次函数综合题、矩形的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．