题目内容
 如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-2,-1),则点A坐标为
如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-2,-1),则点A坐标为考点:正方形的性质,坐标与图形性质,全等三角形的判定与性质
专题:
分析:过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,根据点C的坐标求出OE、CE,再根据正方形的性质可得OA=OC=BC,再求出∠AOD=∠COE=∠BCF,然后求出△AOD、△COE、△BCF全等,根据全等三角形对应边相等可得AD=CE=BF,OD=OE=CF,然后求解即可.
解答: 解:如图,过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,
解:如图,过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,
∵C(-2,-1),
∴OE=2,CE=1,
∵四边形OABC是正方形,
∴OA=OC=BC,
易求∠AOD=∠COE=∠BCF,
又∵∠ODA=∠OEC=∠F=90°,
∴△AOD≌△COE≌△BCF,
∴AD=CE=BF=1,OD=OE=CF=2,
∴点A的坐标为(-1,2),EF=2-1=1,
点B到y轴的距离为1+2=3,
∴点B的坐标为(-3,1).
故答案为:(-1,2);(-3,1).
 解:如图,过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,
解:如图,过点A作AD⊥y轴于D,过点C作CE⊥x轴,过点B作BF⊥CE交CE的延长线于F,∵C(-2,-1),
∴OE=2,CE=1,
∵四边形OABC是正方形,
∴OA=OC=BC,
易求∠AOD=∠COE=∠BCF,
又∵∠ODA=∠OEC=∠F=90°,
∴△AOD≌△COE≌△BCF,
∴AD=CE=BF=1,OD=OE=CF=2,
∴点A的坐标为(-1,2),EF=2-1=1,
点B到y轴的距离为1+2=3,
∴点B的坐标为(-3,1).
故答案为:(-1,2);(-3,1).
点评:本题考查了正方形的性质,全等三角形的判定与性质,坐标与图形性质,熟记各性质是解题的关键,难点在于作辅助线构造出全等三角形.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )| A、159° | B、141° |
| C、111° | D、69° |

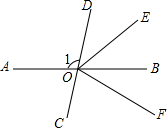 如图所示,直线AB、CD是经同一点O的不同直线,OE是∠BOD的角平分线,OF是∠COE的角平分线,当∠1=100°时,求∠COF的度数.
如图所示,直线AB、CD是经同一点O的不同直线,OE是∠BOD的角平分线,OF是∠COE的角平分线,当∠1=100°时,求∠COF的度数.