题目内容
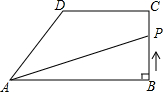 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).当点P在边DA上运动时,则S关于t的函数表达式为
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).当点P在边DA上运动时,则S关于t的函数表达式为考点:动点问题的函数图象
专题:
分析:如图,首先作辅助线求出AD的长度;然后运用相似三角形的判定及其性质表示出QF的长度,问题即可解决.
解答: 解:如图,过点D作DE⊥AB于点E;
解:如图,过点D作DE⊥AB于点E;
当点P运动到点Q的位置时,连接BQ,
过点Q作QF⊥AB于点F;
则四边形DEBC为矩形,
DE=BC=4cm,BE=DC=5cm,
∴AE=8-5=3(cm);
由勾股定理得:
AD2=32+42=25,
∴AD=5(cm);
由题意得:
DQ=t--4-5=t-9,AQ=5-(t-9)=14-t;
∵QF⊥AB,DE⊥AB,
∴QF∥DE,
∴△AQF∽△ADE;
∴
=
,
∴QF=
;
∴S=
AB•QF=
×8×
=-
t+
,
故答案为:S=-
t+
.
 解:如图,过点D作DE⊥AB于点E;
解:如图,过点D作DE⊥AB于点E;当点P运动到点Q的位置时,连接BQ,
过点Q作QF⊥AB于点F;
则四边形DEBC为矩形,
DE=BC=4cm,BE=DC=5cm,
∴AE=8-5=3(cm);
由勾股定理得:
AD2=32+42=25,
∴AD=5(cm);
由题意得:
DQ=t--4-5=t-9,AQ=5-(t-9)=14-t;
∵QF⊥AB,DE⊥AB,
∴QF∥DE,
∴△AQF∽△ADE;
∴
| QF |
| DE |
| AQ |
| AD |
∴QF=
| 4(14-t) |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 4(14-t) |
| 5 |
=-
| 16 |
| 5 |
| 224 |
| 5 |
故答案为:S=-
| 16 |
| 5 |
| 224 |
| 5 |
点评:该命题主要考查了动点问题的函数图象及其应用问题;解题的关键是抓住动点在运动过程中的变化规律,动中求静,以静制动.

练习册系列答案
相关题目
 如图,直线l表示草原的一条河,小明家为A处,小红家为B处,小明从家去发到小红家取钓鱼工具再去河边钓鱼,问小明按怎样的路线使总路程最短?请画出这条路线.
如图,直线l表示草原的一条河,小明家为A处,小红家为B处,小明从家去发到小红家取钓鱼工具再去河边钓鱼,问小明按怎样的路线使总路程最短?请画出这条路线.
 如图,已知线段a,b,c,画一条线段,使它等于a+b-c.
如图,已知线段a,b,c,画一条线段,使它等于a+b-c. 如图,五边形ABCDE是正五边形,AD是对角线,求证:AD∥BC.
如图,五边形ABCDE是正五边形,AD是对角线,求证:AD∥BC.