题目内容
如图，五边形ABCDE是正五边形，AD是对角线，求证：AD∥BC．考点：多边形内角与外角,等腰三角形的性质,正多边形和圆
专题：证明题
分析：根据正五边形的内角和定理，可得正五边形的内角和，根据正五边形的内角相等，可得∠EAB的大小，根据三角形的内角和定理，可得∠EAD的大小，根据角的和差，可得∠BAD的大小，根据平行线的判定，可得答案．
解答：证明：∵五边形ABCDE是正五边形，
∴∠E=∠EAB=∠B=108°，AE=ED，
∴∠EAD=∠EDA
∵三角形内角和定理，
∴∠EAD=（180°-∠E）÷2=（180°-108°）÷2=36°．
∵∠BAD+∠EAD=∠EAB=108°，
∴∠BAD=72°．
∵∠DAB+∠B=108°+72°=180°，
∴AD∥BC．
∴∠E=∠EAB=∠B=108°，AE=ED，
∴∠EAD=∠EDA
∵三角形内角和定理，
∴∠EAD=（180°-∠E）÷2=（180°-108°）÷2=36°．
∵∠BAD+∠EAD=∠EAB=108°，
∴∠BAD=72°．
∵∠DAB+∠B=108°+72°=180°，
∴AD∥BC．
点评：本题考查了多边形内角与外角，利用了正多边形的内角相等，三角形的内角和定理，平行线的判定．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
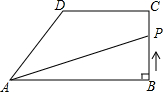如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=8cm．BC=4cm，CD=5cm．动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A．设点P运动的时间为t（s），△PAB面积为S（cm2）．当点P在边DA上运动时，则S关于t的函数表达式为
如图，△ABC为等腰直角三角形，AC=BC，点D在BC的延长线上，BE⊥AD，交AC于M．
如图，△ABC是等腰三角形，D、E分别是腰AB及AC延长线上的点，且DG=GE，请证明：BD=CE．
已知AB⊥BF，DE⊥BF，垂足分别为点B、E，C为BF上的一点，且AB=DE，AC=DF，求证：BE=CF．
如图所示，已知DO⊥CO，∠1=36°，∠3=36°．