题目内容
(1)如图1,点E是正△ABC高AD上的一定点,请在AB上找一点F,使EF=
AE,并说明理由;
(2)如图2,点M是边长为2的正△ABC高AD上的一动点,求
AM+MC的最小值.

| 1 |
| 2 |
(2)如图2,点M是边长为2的正△ABC高AD上的一动点,求
| 1 |
| 2 |

考点:轴对称-最短路线问题,等边三角形的性质,含30度角的直角三角形
专题:
分析:(1)作EF⊥AB,垂足为点F,点F即为所求,根据等边三角形的性质得出∠BAD=30°,根据30°角的直角三角形的性质得出EF=
AE;
(2)根据题意得出C,M,N在一条直线上时,此时
AM+MC最小,进而求得即可.
| 1 |
| 2 |
(2)根据题意得出C,M,N在一条直线上时,此时
| 1 |
| 2 |
解答:解:(1)如图1,作EF⊥AB,垂足为点F,点F即为所求.
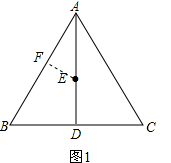
理由如下:∵点E是正△ABC高AD上的一定点,
∴∠BAD=30°,
∵EF⊥AB,
∴EF=
AE;
(2)如图2,作CN⊥AB,垂足为点N,交AD于点M,此时
AM+MC最小,最小为CN的长.
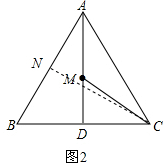
∵△ABC是边长为2的正△ABC,
∴CN=BC•sin60°=2×
=
,
∴MN+CM=
AM+MC=
,
即
AM+MC的最小值为
.

理由如下:∵点E是正△ABC高AD上的一定点,
∴∠BAD=30°,
∵EF⊥AB,
∴EF=
| 1 |
| 2 |
(2)如图2,作CN⊥AB,垂足为点N,交AD于点M,此时
| 1 |
| 2 |

∵△ABC是边长为2的正△ABC,
∴CN=BC•sin60°=2×
| ||
| 2 |
| 3 |
∴MN+CM=
| 1 |
| 2 |
| 3 |
即
| 1 |
| 2 |
| 3 |
点评:此题主要考查了正三角形的性质以及锐角三角函数关系和勾股定理等知识,利用特殊角的三角函数关系得出是解题关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
如果由四舍五入得到的近似数75,那原数不可能是( )
| A、74.48 |
| B、74.53 |
| C、74.87 |
| D、75.49 |
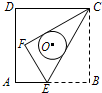 如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( ) 已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).
已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).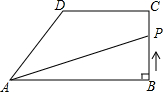 如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).当点P在边DA上运动时,则S关于t的函数表达式为
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=8cm.BC=4cm,CD=5cm.动点P从点B开始沿折线BC-CD-DA以1cm/s的速度运动到点A.设点P运动的时间为t(s),△PAB面积为S(cm2).当点P在边DA上运动时,则S关于t的函数表达式为 已知AB⊥BF,DE⊥BF,垂足分别为点B、E,C为BF上的一点,且AB=DE,AC=DF,求证:BE=CF.
已知AB⊥BF,DE⊥BF,垂足分别为点B、E,C为BF上的一点,且AB=DE,AC=DF,求证:BE=CF.