题目内容
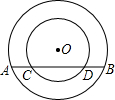 如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是
如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是考点:直线与圆的位置关系
专题:
分析:此题可以首先计算出当AB与小圆相切的时候的弦长.连接过切点的半径和大圆的一条半径,根据勾股定理和垂径定理,得AB=8.则若大圆的弦AB与小圆有两个公共点,即相交,此时AB>8;又大圆最长的弦是直径10,则8<AB≤10.
解答:解:当AB与小圆相切,
∵大圆半径为5cm,小圆的半径为3cm,
∴AB=2
=8cm.
∵大圆的弦AB与小圆有两个公共点,即相交,
∴8<AB≤10.
故答案为:8<AB≤10.
∵大圆半径为5cm,小圆的半径为3cm,
∴AB=2
| 52-32 |
∵大圆的弦AB与小圆有两个公共点,即相交,
∴8<AB≤10.
故答案为:8<AB≤10.
点评:本题综合运用了切线的性质、勾股定理和垂径定理.此题可以首先计算出和小圆相切时的弦长,再进一步分析相交时的弦长.

练习册系列答案
相关题目
反比例函数y=
的图象,当x>0时,y随x的增大而减小,则k的取值范围是( )
| k-2 |
| x |
| A、k<2 | B、k≤2 |
| C、k>2 | D、k≥2 |
 海中有一个小岛A,该岛四周10海里内有暗礁,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?
海中有一个小岛A,该岛四周10海里内有暗礁,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?