题目内容
 海中有一个小岛A,该岛四周10海里内有暗礁,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?
海中有一个小岛A,该岛四周10海里内有暗礁,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行,你认为货轮继续向东航行途中会有触礁的危险吗?考点:解直角三角形的应用-方向角问题
专题:
分析:设AD=x海里,先解Rt△ACD,得出CD=AD•tan25°,再解Rt△ABD,得出BD=AD•tan55°,然后根据BD-CD=BC列出方程,解方程求出A到BC的最短距离,和10比较可得答案.
解答: 解:如图,作AD⊥BC于点D,
解:如图,作AD⊥BC于点D,
在Rt△ACD中,∵∠ADC=90°,∠CAD=25°,
∴CD=AD•tan25°=tan25°•x.
在Rt△ABD中,∵∠ADB=90°,∠BAD=55°,
∴BD=AD•tan55°=tan55°•x.
∵BD-CD=BC,
∴tan55°•x-tan25°•x=20,
∴x=
≈20.79>10,
因为A岛到货轮的航线的最短距离大于10,所以不可能触礁.
 解:如图,作AD⊥BC于点D,
解:如图,作AD⊥BC于点D,在Rt△ACD中,∵∠ADC=90°,∠CAD=25°,
∴CD=AD•tan25°=tan25°•x.
在Rt△ABD中,∵∠ADB=90°,∠BAD=55°,
∴BD=AD•tan55°=tan55°•x.
∵BD-CD=BC,
∴tan55°•x-tan25°•x=20,
∴x=
| 20 |
| tan55°-tan25° |
因为A岛到货轮的航线的最短距离大于10,所以不可能触礁.
点评:本题考查了解直角三角形的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
在数5,-2,7,-6中,任意三个不同的数相加,其中最小的和是( )
| A、10 | B、6 | C、-3 | D、-1 |
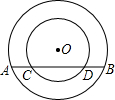 如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是
如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是 若输入的数字为-1,按右图中的程序计算,并求出输出的结果.(写出详细的运算过程)
若输入的数字为-1,按右图中的程序计算,并求出输出的结果.(写出详细的运算过程)