题目内容
反比例函数y=
的图象,当x>0时,y随x的增大而减小,则k的取值范围是( )
| k-2 |
| x |
| A、k<2 | B、k≤2 |
| C、k>2 | D、k≥2 |
考点:反比例函数的性质
专题:
分析:先根据当x>0时,y随x的增大而减小得出关于k的不等式,求出k的取值范围即可.
解答:解:∵反比例函数y=
中,当x>0时,y随x的增大而减小,
∴k-2>0,
解得k>2.
故选C.
| k-2 |
| x |
∴k-2>0,
解得k>2.
故选C.
点评:本题考查的是反比例函数的性质,熟知反比例函数y=
(k≠0)中,当k>0时,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小是解答此题的关键.
| k |
| x |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
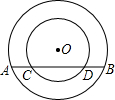 如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是
如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是 若输入的数字为-1,按右图中的程序计算,并求出输出的结果.(写出详细的运算过程)
若输入的数字为-1,按右图中的程序计算,并求出输出的结果.(写出详细的运算过程)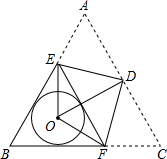 如图,正△ABC的边长为4,⊙O与正△ABC的边AB,BC都相切,点D,E,F分别在边AC,AB,BC上,现将正△ABC沿着DE,DF折叠,点A,点C都恰好落在圆心O处,连接EF,若EF恰好与⊙O相切,则⊙O的半径为
如图,正△ABC的边长为4,⊙O与正△ABC的边AB,BC都相切,点D,E,F分别在边AC,AB,BC上,现将正△ABC沿着DE,DF折叠,点A,点C都恰好落在圆心O处,连接EF,若EF恰好与⊙O相切,则⊙O的半径为