题目内容
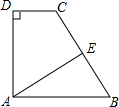 如图,在直角梯形ABCD中,AB∥DC,AE⊥BC于E,BE=CE,AE=4,BC=6,则梯形ABCD的面积是
如图,在直角梯形ABCD中,AB∥DC,AE⊥BC于E,BE=CE,AE=4,BC=6,则梯形ABCD的面积是考点:直角梯形,等腰三角形的判定与性质,勾股定理
专题:
分析:过C作CF⊥AB于F,连接AC,得出平行四边形ADCF,推出AD=CF,DC=AF,根据勾股定理求出AC,根据三角形面积求出CF,根据勾股定理求出DC,根据梯形面积公式求即可.
解答:解: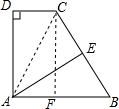
过C作CF⊥AB于F,连接AC,
∵梯形ABCD是直角梯形,
∴AD∥CF,
∵DC∥AB,
∴四边形ADCF是平行四边形,
∴DC=AF,AD=CF,
∵AE⊥BC,BE=CE,
∴AC=AB,BE=CE=
×6=3,∠AEC=90°,
∴在Rt△AEC中,AE=4,CE=3,由勾股定理得:AC=5=AB,
在△ACB中,由三角形面积公式得:BC×AE=AB×CF,
∴6×4=5×CF,
∴CF=
,
∴AD=CF=
,
在Rt△ADC中,由勾股定理得:DC=
=
=
,
∴梯形ABCD的面积是
×(DC+AB)×AD=
×(
+5)×
=
,
故答案为:
.

过C作CF⊥AB于F,连接AC,
∵梯形ABCD是直角梯形,
∴AD∥CF,
∵DC∥AB,
∴四边形ADCF是平行四边形,
∴DC=AF,AD=CF,
∵AE⊥BC,BE=CE,
∴AC=AB,BE=CE=
| 1 |
| 2 |
∴在Rt△AEC中,AE=4,CE=3,由勾股定理得:AC=5=AB,
在△ACB中,由三角形面积公式得:BC×AE=AB×CF,
∴6×4=5×CF,
∴CF=
| 24 |
| 5 |
∴AD=CF=
| 24 |
| 5 |
在Rt△ADC中,由勾股定理得:DC=
| AC2-AD2 |
52-(
|
| 7 |
| 5 |
∴梯形ABCD的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 5 |
| 24 |
| 5 |
| 364 |
| 25 |
故答案为:
| 364 |
| 25 |
点评:本题考查了梯形的性质,勾股定理,三角形的面积的应用,解此题的关键是求出DC、AB、AD饿长,题目是一道综合性比较强的题目,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
判断下列说法正确的是( )
| A、三角形的三条高都在三角形的内部 |
| B、过一点有且只有一条直线与已知直线平行 |
| C、两条直线被第三条直线所截,同旁内角互补 |
| D、平移前后图形的形状和大小都没有发生改变 |
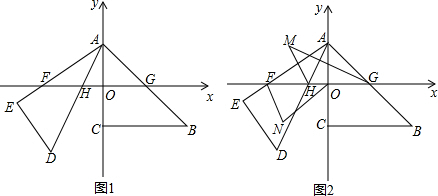
 如图,△ABC中,∠C=90°,CA=CB,E、F分别为CA、CB上一点,CE=CF,M、N分别为AF、BE的中点.求证:AE=
如图,△ABC中,∠C=90°,CA=CB,E、F分别为CA、CB上一点,CE=CF,M、N分别为AF、BE的中点.求证:AE=