题目内容
 如图,△ABC中,∠C=90°,CA=CB,E、F分别为CA、CB上一点,CE=CF,M、N分别为AF、BE的中点.求证:AE=
如图,△ABC中,∠C=90°,CA=CB,E、F分别为CA、CB上一点,CE=CF,M、N分别为AF、BE的中点.求证:AE=| 2 |
考点:三角形中位线定理,等腰直角三角形
专题:证明题
分析:取AB的中点G,连接MG、NG,根据三角形的中位线平行于第三边并且等于第三边的一半可得NG=
AE,NG∥AE,MG=
BF,MG∥BF,再求出AE=BF,∠MGN=90°,判断出△MNG是等腰直角三角形,根据等腰直角三角形的性质可得NG=
MN,再表示出AE即可得证.
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解答: 证明:如图,取AB的中点G,连接MG、NG,
证明:如图,取AB的中点G,连接MG、NG,
∵M、N分别为AF、BE的中点,
∴NG=
AE,NG∥AE,MG=
BF,MG∥BF,
∵CE=CF,∠C=90°,
∴AE=BF,∠MGN=∠C=90°,
∴MG=NG,
∴△MNG是等腰直角三角形,
∴NG=
MN,
∴AE=2NG=NG=
×2MN=
MN,
即AE=
MN.
 证明:如图,取AB的中点G,连接MG、NG,
证明:如图,取AB的中点G,连接MG、NG,∵M、N分别为AF、BE的中点,
∴NG=
| 1 |
| 2 |
| 1 |
| 2 |
∵CE=CF,∠C=90°,
∴AE=BF,∠MGN=∠C=90°,
∴MG=NG,
∴△MNG是等腰直角三角形,
∴NG=
| ||
| 2 |
∴AE=2NG=NG=
| ||
| 2 |
| 2 |
即AE=
| 2 |
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰直角三角形的判定与性质,熟记定理并作辅助线构造成等腰直角三角形是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目


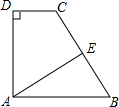 如图,在直角梯形ABCD中,AB∥DC,AE⊥BC于E,BE=CE,AE=4,BC=6,则梯形ABCD的面积是
如图,在直角梯形ABCD中,AB∥DC,AE⊥BC于E,BE=CE,AE=4,BC=6,则梯形ABCD的面积是 已知,如图,AB=AD=5,∠B=15°,CD⊥AB于C,则CD=
已知,如图,AB=AD=5,∠B=15°,CD⊥AB于C,则CD=