题目内容
若矩形的两条对角线的夹角为60°,一条对角线与短边的和为3,则矩形长边的长等于 .
考点:矩形的性质
专题:
分析:根据四边形ABCD是矩形,得到OA=OC,OB=OD,AC=BD,推出OA=OB,根据等边三角形的判定得出△OAB是等边三角形,即可求出AB和对角线长,利用勾股定理即可求出长边的长.
解答:解:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△OAB是等边三角形,
∴AB=OB=OA=
×3=1,
AC=BD=2.
∴BC=
=
,
∴矩形长边的长等于
,
故答案为:
.
∴OA=OC,OB=OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,

∴△OAB是等边三角形,
∴AB=OB=OA=
| 1 |
| 3 |
AC=BD=2.
∴BC=
| 22-1 |
| 3 |
∴矩形长边的长等于
| 3 |
故答案为:
| 3 |
点评:本题主要考查对矩形的性质,等边三角形的性质和判定以及勾股定理等知识点的理解和掌握,能根据性质得到等边三角形OAB是解此题的关键,题型较好,难度适中.

练习册系列答案
相关题目
在代数式①
;②
;③
;④
中,属于分式的有( )
| 1 |
| x |
| a+b |
| 5 |
| 1 |
| 2-m |
| 1 |
| π-1 |
| A、①② | B、①③ |
| C、①③④ | D、①②③④ |

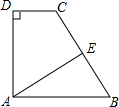 如图,在直角梯形ABCD中,AB∥DC,AE⊥BC于E,BE=CE,AE=4,BC=6,则梯形ABCD的面积是
如图,在直角梯形ABCD中,AB∥DC,AE⊥BC于E,BE=CE,AE=4,BC=6,则梯形ABCD的面积是