题目内容
已知:关于x的方程mx2+(3m+1)x+3=0.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)如果该方程有两个不同的整数根,且m为正整数,求m的值;
(3)在(2)的条件下,令y=mx2+(3m+1)x+3,如果当x1=a与x2=a+n(n≠0)时有y1=y2,求代数式4a2+12an+5n2+16n+8的值.
解:(1)当m=0时,原方程化为x+3=0,此时方程有实数根 x=-3.…………1分
当m≠0时,原方程为一元二次方程.
∵△=(3m+1)2-12m=9m2-6m+1=(3m-1)2.
∵m≠0,∴不论m为任何实数时总有(3m-1)2≥0.
∴此时方程有两个实数根.………………………………………………2分
综上,不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根.
(2)∵mx2+(3m+1)x+3=0.
解得 x1=-3,x2=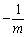 . ………………………………………………3分
. ………………………………………………3分
∵方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,
∴m=1.………………………………………………………………………5分
(3)∵m=1,y=mx2+(3m+1)x+3.
∴y=x2+4x+3.
又∵当x1=a与x2=a+n(n≠0)时有y1=y2,
∴当x1=a时,y1=a2+4a+3,
当x2=a+n时,y2=(a+n)2+4(a+n)+3.
∴a2+4a+3=(a+n)2+4(a+n)+3.
化简得 2an+n2+4n=0.
即 n(2a+n+4)=0.
又∵n≠0,∴2a=-n-4.
∴ 4a2+12an+5n2+16n+8
=(2a)2+2a•6n+5n2+16n+8
=(n+4)2+6n(-n-4)+5n2+16n+8=24.

练习册系列答案
相关题目


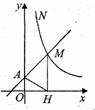 如图,直线y=x+1与y轴交于A点,与反比列函数y=
如图,直线y=x+1与y轴交于A点,与反比列函数y= (x>
(x>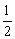 .
.
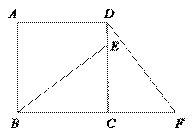


 = ,
= , 数;
数; 、
、 是
是 的
的 边上的两点,且
边上的两点,且 ,则
,则 的大小为( ) A.
的大小为( ) A. B.
B. C.
C. D.
D.
