题目内容
已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)如果BC+DF=9,CF=3,求正方形ABCD的面积.
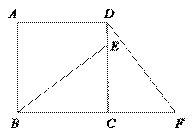
(1)证明:∵正方形ABCD,
∴BC=CD,∠BCE=∠DCF=90°.
又∵CE=CF,
∴△BEC≌△DFC(SAS). ……………4分
(2)解:设BC=x,则CD=x,DF=9-x,
在Rt△DCF中,∵∠DCF=90°,CF=3,
∴CF2+CD2=DF2.
∴32+x2=(9-x)2.
解得x=4.
∴正方形ABCD的面积为:4×4=16.
 |

练习册系列答案
相关题目
 (x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△A B'C,B'点落在OA上,则四边形OABC的面积是( )
(x<0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴负半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△A B'C,B'点落在OA上,则四边形OABC的面积是( )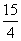 D. 4
D. 4

 B.16 C.
B.16 C. D.8
D.8
 ,当
,当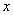 的值减小1,
的值减小1, 的值就减小2,则当
的值就减小2,则当