题目内容
17．
在△ABC中，∠A=120°，AB=4，AC=2，求sinB的值．
分析 作CD⊥AB于D，则∠DAC=60°，在△ADC中，求得AC=2，得AD=1，CD=$\sqrt{3}$，再由勾股定理得出BD=5，BC即可．
解答 
解：作CD⊥AB于D，
∴∠ADC=90°，
∵∠A=120°，
∴∠DAC=180°-∠A=60°，
在△ADC中，AC=2，
可得AD=1，CD=$\sqrt{3}$，
∴BD=5，
在△BCD中，BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=2$\sqrt{7}$．
∴sinB=$\frac{CD}{BC}$=$\frac{\sqrt{3}}{2\sqrt{7}}$=$\frac{\sqrt{21}}{14}$．
点评 本题考查了解直角三角形，以及勾股定理，熟记三角函数的定义是解题的关键．
练习册系列答案
相关题目
如图所示，AD∥BC，∠A=∠C，求∠AFB+∠CEA的度数．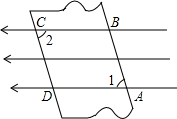
如图，在一束平行光线中插入一张对边平行的纸板，如果光线与纸板右下方所成的∠1是72°15′，那么光线与纸板左上方所成的∠2是多少度？为什么？
△ABC中，∠B=30°，AB=8cm，BC=4cm，则△ABC的面积为8cm2．
9．下列图形中，旋转120°后能与原图形重合的是（ ）
| A． | 等边三角形 | B． | 正方形 | C． | 正五边形 | D． | 正八边形 |
