题目内容
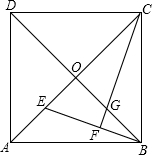 如图,已知正方形ABCD的对角线AC、BD相交于点O,BE平分∠OBA,CF⊥BE于F,交OB于G.
如图,已知正方形ABCD的对角线AC、BD相交于点O,BE平分∠OBA,CF⊥BE于F,交OB于G.(1)求证:OE=OG.
(2)若E在O、A两点之间运动(不与O、A重合),CF保持与BE的垂直关系,那么OE与OG还相等吗?(不需要证明)
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形对角线平分一组对角和角平分线的定义求出∠OBE=22.5°,再求出∠OCG=22.5°,从而得到∠OBE=∠OCG,再根据正方形的对角线互相平分且相等求出OB=OC,然后利用“角边角”证明△OBE和△OCG全等,根据全等三角形对应边相等可得OE=OG;
(2)根据同角的余角相等求出∠OBE=∠OCG,再利用“角边角”证明△OBE和△OCG全等,根据全等三角形对应边相等可得OE=OG.
(2)根据同角的余角相等求出∠OBE=∠OCG,再利用“角边角”证明△OBE和△OCG全等,根据全等三角形对应边相等可得OE=OG.
解答:(1)证明:∵正方形ABCD中,BE平分∠OBA,
∴∠OBE=22.5°,
∵AC⊥BD,CF⊥BE,
∴∠OCG=22.5°,
∴∠OBE=∠OCG,
∵四边形ABCD是正方形,
∴OB=OC,∠BOE=∠COG=90°,
在△OBE和△OCG中,
,
∴△OBE≌△OCG(ASA),
∴OE=OG;
(2)解:OE=OG.
理由如下:∵AC⊥BD,CF⊥BE,
∴∠OCG+∠OEB=90°,∠OBE+∠OEB=90°,
∴∠OBE=∠OCG,
∵四边形ABCD是正方形,
∴OB=OC,∠BOE=∠COG=90°,
在△OBE和△OCG中,
,
∴△OBE≌△OCG(ASA),
∴OE=OG.
∴∠OBE=22.5°,
∵AC⊥BD,CF⊥BE,
∴∠OCG=22.5°,
∴∠OBE=∠OCG,
∵四边形ABCD是正方形,
∴OB=OC,∠BOE=∠COG=90°,
在△OBE和△OCG中,
|
∴△OBE≌△OCG(ASA),
∴OE=OG;
(2)解:OE=OG.
理由如下:∵AC⊥BD,CF⊥BE,
∴∠OCG+∠OEB=90°,∠OBE+∠OEB=90°,
∴∠OBE=∠OCG,
∵四边形ABCD是正方形,
∴OB=OC,∠BOE=∠COG=90°,
在△OBE和△OCG中,
|
∴△OBE≌△OCG(ASA),
∴OE=OG.
点评:本题考查了正方形的性质,全等三角形的判定与性质,熟记性质并确定出全等三角形和三角形全等的条件是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列图形中,是轴对称图形是( )
A、 |
B、 |
C、 |
D、 |
一个长方形的长与宽分别时6cm、5cm,它的对角线的长可能是( )
| A、整数 | B、分数 |
| C、有理数 | D、无理数 |
 去年冬季我国内蒙古部分牧遭受严重雪灾,空军某部奉命赴灾区空投救灾物资.已知空投物资离开飞机后,在空中沿抛物线的顶点在机舱舱口A处.
去年冬季我国内蒙古部分牧遭受严重雪灾,空军某部奉命赴灾区空投救灾物资.已知空投物资离开飞机后,在空中沿抛物线的顶点在机舱舱口A处.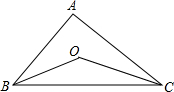 已知:如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O.
已知:如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O. 如图,直线a上有5个点,A1,A2,…,A5,图中共有多少个三角形?
如图,直线a上有5个点,A1,A2,…,A5,图中共有多少个三角形? △ABC和△FED中,AD=FC,∠A=∠F.当添加条件
△ABC和△FED中,AD=FC,∠A=∠F.当添加条件