题目内容
12.△ABC的高AD长为3,且BD=6,CD=2,则△ABC的面积是12或6.分析 根据三角形的面积公式计算即可.
解答 解:如图1:
所以三角形ABC的面积=$\frac{1}{2}(BD+DC)•AD=\frac{1}{2}×(6+2)×3=12$;
如图2:
所以三角形ABC的面积=$\frac{1}{2}$(BD-CD)•AD=$\frac{1}{2}$×(6-2)×3=6.
故答案为:12或6.
点评 此题考查三角形的面积,关键是根据题意画出图形,再根据三角形面积公式计算.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
3.若一组数据3,5,7,8,x,11的众数是5,则这组数据的中位数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7.5 |
17.下列计算正确的是( )
| A. | a2•a4=a8 | B. | (a+b)(a-2b)=a2-2b2 | C. | 5a-2a=3 | D. | (ab3)2=a2b6 |
1.下列式子运算正确的是( )
| A. | a6÷a2=a4 | B. | a2+a3=a5 | C. | (a+1)2=a2+1 | D. | 3a-2a=1 |
17.关于x的二次函数y=-(x-1)2+2,下列说法正确的是( )
| A. | 当x>1时,y随x的增大而减小 | B. | 图象与y轴的交点坐标为(0,2) | ||
| C. | 图象的开口向上 | D. | 图象的顶点坐标是(-1,2) |

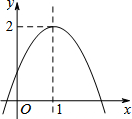 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论: