题目内容
 已知:如图,⊙O的弦AB长为8,延长AB至C,使BC=AB,tanC=
已知:如图,⊙O的弦AB长为8,延长AB至C,使BC=AB,tanC=| 1 |
| 4 |
求:
(1)⊙O的半径;
(2)点C到直线AO的距离.
考点:垂径定理,解直角三角形
专题:
分析:(1)作OD⊥AB,垂足为点,求出AD、CD,根据勾股定理求出AO即可;
(2)解直角三角形即可求出答案.
(2)解直角三角形即可求出答案.
解答:解:(1)作OD⊥AB,垂足为点D,
由垂径定理,得AD=BD,
∵BC=AB=8,
∴AD=4,CD=12,
∵tanC=
,
∴OD=3,
∴AO=5,
由勾股定理得:AO=
=5,
即⊙O的半径等于5;
(2)作CE⊥AO,垂足为点E,
∵sinA=
=
,
∴
=
,
解得CE=
,
∴点C到直线AO的距离是
.

由垂径定理,得AD=BD,
∵BC=AB=8,
∴AD=4,CD=12,
∵tanC=
| 1 |
| 4 |
∴OD=3,
∴AO=5,
由勾股定理得:AO=
| 42+32 |
即⊙O的半径等于5;
(2)作CE⊥AO,垂足为点E,

∵sinA=
| CE |
| AC |
| OD |
| AO |
∴
| CE |
| 16 |
| 3 |
| 5 |
解得CE=
| 48 |
| 5 |
∴点C到直线AO的距离是
| 48 |
| 5 |
点评:本题考查了垂径定理,解直角三角形,勾股定理的应用,主要考查学生运用定理进行推理和计算的能力,题目比较典型,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 如图,已知正比例函数
如图,已知正比例函数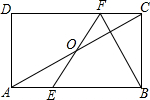 如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
如图,在矩形ABCD中,E、F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC. 将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x、y均为整数.如数5对应的坐标为(-1,1),则2014对应的坐标是
将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x、y均为整数.如数5对应的坐标为(-1,1),则2014对应的坐标是