题目内容
12.已知:?ABCD的两边AB,AD的长是关于x的方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.(1)当m为何值时,?ABCD是菱形?
(2)若AB的长为2,那么?ABCD的周长是多少?
分析 (1)直接利用菱形性质结合根的判别式求出m的值;
(2)利用AB=2,代入方程求出m的值,进而解方程得出x的值,再利用平行四边形的性质得出答案.
解答 解:(1)∵?ABCD是菱形,
∴AB=AD,
∴△=b2-4ac=(-m)2-4×1×($\frac{m}{2}$-$\frac{1}{4}$)
=m2-2m+1
=(m-1)2=0,
解得:m=1,
即m为1时,?ABCD是菱形;
(2)把AB=2代入方程得:
4-2m+$\frac{m}{2}$-$\frac{1}{4}$=0,
解得:m=$\frac{5}{2}$,
则x2-$\frac{5}{2}$x+1=0,
解得:x1=$\frac{1}{2}$,x2=2,
则AD=$\frac{1}{2}$,
故?ABCD的周长是:2×(2+$\frac{1}{2}$)=5.
点评 此题主要考查了菱形的性质以及平行四边形的性质以及一元二次方程的解法和根的判别式等知识,正确掌握菱形的性质是解题关键.

练习册系列答案
相关题目
1.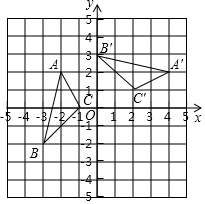 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )| A. | (0,1) | B. | (0,-1) | C. | C(1,-1) | D. | (1,0) |

 如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).
如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).