题目内容
已知一个二次函数的关系式为 y=x2-2bx+c.
(1)若该二次函数的图象与x轴只有一个交点,
①则b、c 应满足关系为 ;
②若该二次函数的图象经过A(m,n)、B(m +6,n)两点,求n的值;
(2)若该二次函数的图象与x轴有两个交点C(6,0)、D(k,0),线段CD(含端点)上有若干个横坐标为整数的点,且这些点的横坐标之和为21,求b的取值范围.
(1)(1)①c=b2;
②解法一:由 ,
,
得b=m +3,则c=(m +3)2
于是,n=m 2-2(m +3)m+(m +3)2=9;
解法二:
由题意可知:y=x2-2bx+c的图象是由y=x2的图象沿x轴平移得到的,
∵y=x2-2bx+c的图象经过A(m,n)、B(m +6,n)两点,
∴y=x2的图象经过(-3,n)、(3,n)两点,
∴n=32=6.
(2)解法一:∵y=x2-2bx+c图象与x轴交于C(6,0)
∴36 -12b+c=0,∴ c=12b -36
∴y=x2-2bx+12b -36,令y=0得x2-2bx+12b -36=0
解得: x1=6,x2=2b – 6,即k=2b - 6;
∵C、D之间的整数和为21,
∴由8≤k<9,或-1<k≤1,
∴8≤2b-6<9,或-1<2b- 6≤1,
6≤1,
解得7≤b<7.5或2.5<b≤3.5.
解法二:∵y=x2-2bx+c图象过C(6,0)与D(k,0),
∴(x -6)(x – k)=0,整理得x2 -(6+ k)x+6k=0
∴6+k=2b ,k=2b - 6;
∵C、D之间的整数和为21,
∴由8≤k<9,或-1<k≤1,
∴8≤2b-6<9,或-1<2b-6≤1,
解得7≤b<7.5或2.5<b≤3.5.
解法三:∵ =b,∴k=2b – 6
=b,∴k=2b – 6
∵C、D之间的整数和为21,
∴由8≤k<9,或-1<k≤1,
∴8≤2b-6<9,或-1<2b-6≤1,
解得7≤b<7.5或2.5<b≤3.5.

某商店经销甲、乙两种 商品. 现有如下信息:
商品. 现有如下信息:
 |
请根据以上信息,解答下列问题:
(1)求甲、乙两种商品的零售单价;
(2)该商店平均每天卖出甲商品500件和乙商品1200件.经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.商店决定把甲种商品的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m为多少时,商店每天销售甲、乙两种商品获取的总利润为1700元?
 ,0),B(
,0),B( ,
, )
)



 B.y=
B.y= C.y=
C.y= D.y=
D.y=
 的中点M重合,折痕为EF;
的中点M重合,折痕为EF;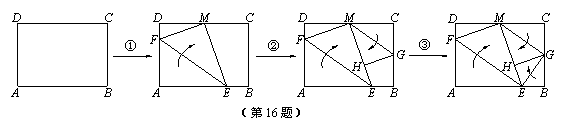 ③翻折纸片,使B落在ME上,点B的对应点恰与H重合,折痕为GE.
③翻折纸片,使B落在ME上,点B的对应点恰与H重合,折痕为GE.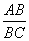 = .
= .