题目内容
3.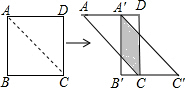 如图,将边长为4的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′.
如图,将边长为4的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′.(1)当两个三角形重叠部分的面积为3时,求移动的距离AA′;
(2)当移动的距离AA′是何值时,重叠部分是菱形.
分析 (1)设AC、A′B′交于点E,DC、A′C′交于点F,且设AA′=x,则A′E=AA′=x,A′D=4-x,列出方程即可解决问题;
(2)当四边形A′ECF是菱形时,A′E=A′F,设AA′=x,则A′E=CF=x,根据A′F2=2A′D2列出方程即可解决问题;
解答 解:(1)设AC、A′B′交于点E,DC、A′C′交于点F,
且设AA′=x,则A′E=AA′=x,A′D=4-x,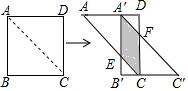
重叠部分的面积为x(4-x)
由x(4-x)=3,
解得x=1或3,
即AA′=1或3.
(2)当四边形A′ECF是菱形时,A′E=A′F,
设AA′=x,则A′E=CF=x,
∴A′F2=2A′D2,
∴x2=2(4-x)2,
∴x=8-4$\sqrt{2}$或8+4$\sqrt{2}$(舍弃),
即当移动的距离是8-4$\sqrt{2}$时,重叠部分是菱形.
点评 本题考查正方形的性质、菱形的判定和性质、平移的性质等知识,解题的关键是学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.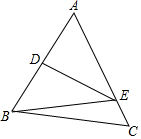 如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )
如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )
 如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )
如图,在△ABC中,BC=4cm,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于9cm,则AC的长等于( )| A. | 3 cm | B. | 4 cm | C. | 5 cm | D. | 6 cm |
12.矩形具有而菱形不一定具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对边相等 | D. | 对角线相等 |
13.已知整式x2-2x的值为6,则代数式5-2x2+4x的值为( )
| A. | 8 | B. | -7 | C. | 11 | D. | -17 |
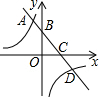 如图,已知函数y=-x+2的图象与x轴、y轴分别交于点C、B,与双曲线y=$\frac{k}{x}$交于点A、D,若AB+CD=BC,则k的值为-3.
如图,已知函数y=-x+2的图象与x轴、y轴分别交于点C、B,与双曲线y=$\frac{k}{x}$交于点A、D,若AB+CD=BC,则k的值为-3.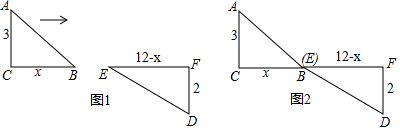
 如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数至少4个.
如图,分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图,则组成这个物体的小正方体的个数至少4个.