题目内容
13.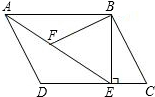 如图,在平行四边形ABCD中,过点B作BE⊥CD于E点,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD于E点,连接AE,F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长;
(3)在(1)(2)的条件下,若AD=3,求BF的长.
分析 (1)根据两角相等,即∠AFB=∠ADE和∠BAE=∠AED,证明△ABF∽△EAD;
(2)在Rt△ABE中,利用30°的余弦得AE的长;
(3)由相似得:$\frac{BF}{AD}=\frac{AB}{AE}$,代入可求得BF的长.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠ADE=180°,
∵∠BFE=∠C,
∴∠BFE+∠ADE=180°,
∵∠BFE+∠AFB=180°,
∴∠AFB=∠ADE,
∵AB∥DC,
∴∠BAE=∠AED,
∴△ABF∽△EAD;
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,
∵BE⊥DC,
∴BE⊥AB,
∴∠ABE=90°,
在Rt△ABE中,
∵AB=4,∠BAE=30°,
∴cos∠BAE=cos30°=$\frac{AB}{AE}$,
∴AE=$\frac{AB}{cos30°}$=$\frac{4}{\frac{\sqrt{3}}{2}}$=$\frac{8\sqrt{3}}{3}$;
(3)∵△ABF∽△EAD,
∴$\frac{BF}{AD}=\frac{AB}{AE}$,
∴$\frac{BF}{3}=\frac{4}{\frac{8\sqrt{3}}{3}}$,
∴BF=$\frac{3\sqrt{3}}{2}$.
点评 本题是相似形的综合题,难度适中,考查了三角形相似的判定和性质,在相似的判定中,常运用平行和两角对应相等证明两三角形相似;再求线段的长时,可以利用勾股定理来求,有时也会根据相似得比例式代入求解,也可以利用三角函数列式计算求得.

练习册系列答案
相关题目
3.为了倡导节约用水,某城市自来水实行阶梯水价收费,收费标准如表:
(1)若月用水量为x吨,试分别写出当x≤10、10<x≤18、x>18时水费的代数式(用含x的式子表示);
(2)若某户居民3月份的水费为25元,该用户这个月用水量为多少吨?
| 月用水量 | 不超过10吨 | 超过10吨但不超过18吨的部分 | 超过18吨的部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
(2)若某户居民3月份的水费为25元,该用户这个月用水量为多少吨?
8. 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交与点E,与DC交于点F,且DF:CF=3:1,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交与点E,与DC交于点F,且DF:CF=3:1,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交与点E,与DC交于点F,且DF:CF=3:1,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交与点E,与DC交于点F,且DF:CF=3:1,DG⊥AE,垂足为G,若DG=1,则AE的长为( )| A. | 12$\sqrt{2}$ | B. | $\frac{16\sqrt{2}}{3}$ | C. | 3$\sqrt{10}$ | D. | 8 |
18.16的平方根是( )
| A. | 4 | B. | ±4 | C. | $\sqrt{4}$ | D. | ±$\sqrt{4}$ |
5.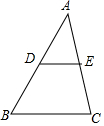 如图,在△ABC中,DE∥BC,且AE=CE,则△ADE与四边形DBCE的面积之比等于( )
如图,在△ABC中,DE∥BC,且AE=CE,则△ADE与四边形DBCE的面积之比等于( )
 如图,在△ABC中,DE∥BC,且AE=CE,则△ADE与四边形DBCE的面积之比等于( )
如图,在△ABC中,DE∥BC,且AE=CE,则△ADE与四边形DBCE的面积之比等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |