题目内容
5.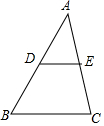 如图,在△ABC中,DE∥BC,且AE=CE,则△ADE与四边形DBCE的面积之比等于( )
如图,在△ABC中,DE∥BC,且AE=CE,则△ADE与四边形DBCE的面积之比等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 因为DE∥BC,所以可得△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方解答即可.
解答 解:∵DE∥BC
∴△ADE∽△ABC,
∴AE:AC=DE:BC,
∵AE=CE,
∴DE:BC=1:2,
∴△ADE与△ABC的面积之比是1:4,
∴△ADE与四边形DBCE的面积之比是1:3.
故选C.
点评 本题考查了相似三角形的判定与性质,熟记相似三角形面积的比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
15.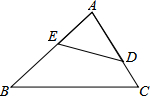 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )
 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )| A. | $\frac{AE}{AC}=\frac{AD}{AB}$ | B. | ∠B=∠ADE | C. | ∠C=∠AED | D. | $\frac{AE}{AC}=\frac{DE}{BC}$ |
16.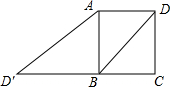 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么AD′为( )
如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么AD′为( )
 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么AD′为( )
如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么AD′为( )| A. | $\sqrt{10}$ | B. | $\sqrt{8}$ | C. | $\sqrt{7}$ | D. | $\sqrt{12}$ |
10.某市区某天的最高气温是8℃,最低气温是零下4℃,则该地这一天的温差是( )
| A. | -10℃ | B. | -8℃ | C. | 8℃ | D. | 12℃ |
14.下列各图不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
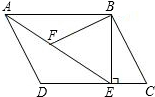 如图,在平行四边形ABCD中,过点B作BE⊥CD于E点,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD于E点,连接AE,F为AE上一点,且∠BFE=∠C.