题目内容
13. 如图,将⊙O的内接矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结BC1,若∠ACB=30°,AB=1,CC1=x.
如图,将⊙O的内接矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结BC1,若∠ACB=30°,AB=1,CC1=x.(1)若点O与点C1重合,求证:A1D1为⊙O的切线;
(2)①当x=1时,四边形ABC1D1是菱形;
②当x=2时,△BDD1为等边三角形.
分析 (1)根据矩形的性质,得∠DAC=∠ACB,再由平移的性质,可得出∠A1=∠ACB,A1D1=CB,从而证出结论;
(2)①根据菱形的性质,四条边都相等,可推得当C1在AC中点时四边形ABC1D1是菱形;
②当x=2时,点C1与点A重合,可求得BD=DD1=BD1=2,从而可判断△BDD1为等边三角形.
解答 解:(1)∵四边形ABCD为矩形,
∴∠D=90°
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠A1D1O=∠D=90°,
∴A1D1⊥OD1,
∴A1D1为⊙O的切线;
(2)当x=1时,四边形ABC1D1是菱形;
理由:∵∠ACB=30°,
∴∠CAB=60°,
∵AB=1,
∴AC=2,
∵x=1,
∴AC1=1,∴AB=AC1,
∴△AC1B是等边三角形,
∴AB=D1C1,
又AB∥D1C1,
∴四边形ABC1D1是菱形;
②如图所示:当x=2时,△BDD1为等边三角形,
则可得BD=DD1=BD1=2,
即当x=2时,△BDD1为等边三角形.
故答案为:1,2.
点评 本题考查了相似三角形的判定与性质、矩形的性质、等边三角形的判定及解直角三角形的知识,解答本题需要我们熟练掌握全等三角形的判定及含30°角的直角三角形的性质,有一定难度.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
1.某市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A,B,C,D,E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.

调查测试成绩分组表
请你根据图中提供的信息解答以下问题:
(1)参加调查测试的学生为400人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩的中位数落在C组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2 600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.

调查测试成绩分组表
| A组:90≤x≤100 |
| B组:80≤x<90 |
| C组:70≤x<80 |
| D组:60≤x<70 |
| E组:x<60 |
(1)参加调查测试的学生为400人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩的中位数落在C组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2 600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
2.一组数据8,3,8,6,7,8,7的众数和中位数分别是( )
| A. | 8,6 | B. | 7,6 | C. | 7,8 | D. | 8,7 |
3.分解因式a2b-b3结果正确的是( )
| A. | b(a+b)(a-b) | B. | b(a-b)2 | C. | b(a2-b2) | D. | b(a+b)2 |
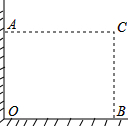 在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.