题目内容
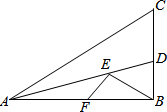 如图,在Rt△ABC中,AC=6,AB=3
如图,在Rt△ABC中,AC=6,AB=3| 3 |
考点:轴对称-最短路线问题
专题:
分析:作FG⊥AD交AC于点G,交AD于点Q,作BH⊥AC,易证∠BAD=∠CAD,即可证明△AQG≌△AQF,可得AF=AG,即可证明△AEF≌△AEG,可得EG=EF,即可求得BE+EF=BG,根据BG最短为BH即可解题.
解答:解:作FG⊥AD交AC于点G,交AD于点Q,作BH⊥AC,

∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△AQG和△AQF中,
,
∴△AQG≌△AQF(ASA),
∴AF=AG,
在△AEF和△AEG中,
,
∴△AEF≌△AEG(SAS),
∴EG=EF,
∴BE+EF=BE+EG=BG,
∵BG最短为BH,
∴BE+EF最短为BH,
∵AB=3
,∠BAC=30°,
∴BH=
AB=
,
故答案为
.

∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△AQG和△AQF中,
|
∴△AQG≌△AQF(ASA),
∴AF=AG,
在△AEF和△AEG中,
|
∴△AEF≌△AEG(SAS),
∴EG=EF,
∴BE+EF=BE+EG=BG,
∵BG最短为BH,
∴BE+EF最短为BH,
∵AB=3
| 3 |
∴BH=
| 1 |
| 2 |
3
| ||
| 2 |
故答案为
3
| ||
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了30°角所对直角边是斜边一半的性质,本题中求证△AQG≌△AQF和△AEF≌△AEG是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
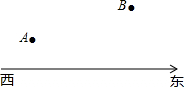 如图,两所学校位于A、B两处,且在一条东西走向公路的同旁,一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有,请用尺规作图找出该点,保留作图痕迹.
如图,两所学校位于A、B两处,且在一条东西走向公路的同旁,一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有,请用尺规作图找出该点,保留作图痕迹.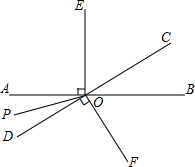 如图,直线AB与CD相交于点O,OP是∠AOD的平分线,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OP是∠AOD的平分线,OE⊥AB,OF⊥CD. 数学活动课上,老师在黑板上画直线l平行于射线AN(如图),让同学们在直线L和射线AN上各找一点B和C,使得以A、B、C为顶点的三角形是等腰直角三角形.这样的三角形最多能画( )
数学活动课上,老师在黑板上画直线l平行于射线AN(如图),让同学们在直线L和射线AN上各找一点B和C,使得以A、B、C为顶点的三角形是等腰直角三角形.这样的三角形最多能画( )