题目内容
)直线y=﹣ x﹣1与反比例函数
x﹣1与反比例函数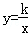 (x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
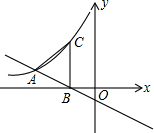
 x﹣1与反比例函数
x﹣1与反比例函数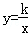 (x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
| A.﹣2 | B.﹣4 | C.﹣6 | D.﹣8 |
B
试题分析:过A作AD⊥BC于D,先求出直线=﹣
 x﹣1与x轴交点B的坐标(﹣2,0),则得到C点的横坐标为﹣2,由于C点在反比例函数y=
x﹣1与x轴交点B的坐标(﹣2,0),则得到C点的横坐标为﹣2,由于C点在反比例函数y=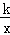 的图象上,可表示出C点坐标为(﹣2,﹣
的图象上,可表示出C点坐标为(﹣2,﹣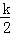 ),利用等腰三角形的性质,由AC=AB,AD⊥BC,得到DC=DB,于是D点坐标为(﹣2,﹣
),利用等腰三角形的性质,由AC=AB,AD⊥BC,得到DC=DB,于是D点坐标为(﹣2,﹣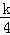 ),则可得到A点的纵坐标为﹣
),则可得到A点的纵坐标为﹣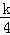 ,利用点A在函数y=
,利用点A在函数y=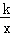 的图象上,可表示出点A的坐标为(﹣4,﹣
的图象上,可表示出点A的坐标为(﹣4,﹣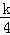 ),然后把A(﹣4,﹣
),然后把A(﹣4,﹣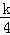 )代入y=﹣
)代入y=﹣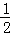 x﹣1得到关于k的方程,解方程即可求出k的值.
x﹣1得到关于k的方程,解方程即可求出k的值.解:过A作AD⊥BC于D,如图,
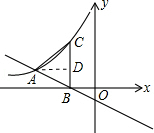
对于y=﹣
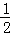 x﹣1,令y=0,则﹣
x﹣1,令y=0,则﹣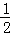 x﹣1=0,解得x=﹣2,
x﹣1=0,解得x=﹣2,∴B点坐标为(﹣2,0),
∵CB⊥x轴,
∴C点的横坐标为﹣2,
对于y=
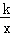 ,令x=﹣2,则y=﹣
,令x=﹣2,则y=﹣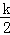 ,
,∴C点坐标为(﹣2,﹣
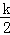 ),
),∵AC=AB,AD⊥BC,
∴DC=DB,
∴D点坐标为(﹣2,﹣
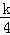 ),
),∴A点的纵坐标为﹣
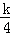 ,
,而点A在函数y=
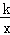 的图象上,
的图象上,把y=﹣
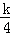 代入y=
代入y=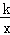 得x=﹣4,
得x=﹣4,∴点A的坐标为(﹣4,﹣
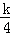 ),
),把A(﹣4,﹣
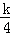 )代入y=﹣
)代入y=﹣ x﹣1得﹣
x﹣1得﹣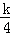 =﹣
=﹣ ×(﹣4)﹣1,
×(﹣4)﹣1,∴k=﹣4.
故选B.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两个函数的解析式.也考查了与x轴垂直的直线上所有点的横坐标相同以及等腰三角形的性质.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
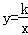 与直线
与直线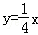 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线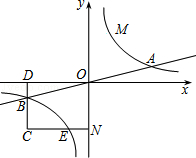
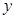 轴的正半轴上,点A在反比例函数
轴的正半轴上,点A在反比例函数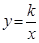 (
(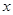 >0)的图象上,点D的坐标为(4,3).
>0)的图象上,点D的坐标为(4,3).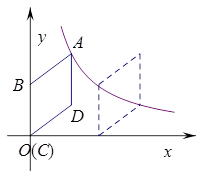
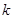 的值;
的值; ,x与y的对应值如下表:
,x与y的对应值如下表: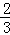 1 2 ﹣2 ﹣1 ﹣
1 2 ﹣2 ﹣1 ﹣
 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x轴于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
 的图象中,阴影部分的面积不等于4的是( )
的图象中,阴影部分的面积不等于4的是( )



 ,
, 的图象和一个圆,则S阴影=( )
的图象和一个圆,则S阴影=( )