题目内容
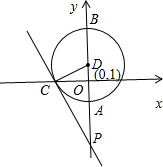 已知,如图,⊙D交y轴于A、B,交x轴于C,过C的直线:y=-2
已知,如图,⊙D交y轴于A、B,交x轴于C,过C的直线:y=-2| 2 |
(1)求证:PC是⊙D的切线;
(2)判断在直线PC上是否存在点E,使得S△EOC=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
分析:(1)求证PC是⊙D的切线,可以先连接DC然后证明垂直即可,由CP所在直线的解析式,我们可得出C,P两点的坐标,就能得出DP,CP的长,只需要求出CD的长.根据勾股定理判定三角形DCP是否为直角三角形即可,那么关键是求出DC的长,有了D的坐标,也求出了C的坐标,那么CD的长就能求出来了.
(2)由于三角形OCD和OCE公用了一条OC边,那么比较它们的面积只需比较E,D两点的纵坐标的绝对值即可.根据S△EOC=4S△CDO,那么E点的纵坐标必为4或-4;根据CP的函数式,可以求出E点的横坐标,这样就能求出E点的坐标了.
(2)由于三角形OCD和OCE公用了一条OC边,那么比较它们的面积只需比较E,D两点的纵坐标的绝对值即可.根据S△EOC=4S△CDO,那么E点的纵坐标必为4或-4;根据CP的函数式,可以求出E点的横坐标,这样就能求出E点的坐标了.
解答:(1)解:∵PC的直线方程为:y=-2
x-8,
∴C(-2
,0),P(0,-8).
∴OC=2
,OP=8,
PC=
=
=6
,
CD=
=
=3,
PD=OP+OD=8+1=9,
PD2=92=81,CD2+PC2=9+72=81.
∴PD2=CD2+PC2.
∴△DCP为直角三角形,∠DCP=90°,DC⊥PC,CD为半径.
∴PC为⊙D的切线.
(2)解:设E(r,y),
∴S△OCE=4S△CDO.
∴
×OC×|y|=4×
OC×OD,
|y|=4OD=4.
∴y=±4,
E1(-3
,4),E2(-
,-4).
| 2 |
∴C(-2
| 2 |
∴OC=2
| 2 |
PC=
| OC2+OP2 |
| 8+64 |
| 2 |
CD=
| OD2+OC2 |
| 1+8 |
PD=OP+OD=8+1=9,
PD2=92=81,CD2+PC2=9+72=81.
∴PD2=CD2+PC2.
∴△DCP为直角三角形,∠DCP=90°,DC⊥PC,CD为半径.
∴PC为⊙D的切线.
(2)解:设E(r,y),
∴S△OCE=4S△CDO.
∴
| 1 |
| 2 |
| 1 |
| 2 |
|y|=4OD=4.
∴y=±4,
E1(-3
| 2 |
| 2 |
点评:本题考查了一次函数和几何问题的综合应用,本题中根据点的坐标求出点与点的距离是解题的基础.

练习册系列答案
相关题目
 ,D两点.
,D两点. P,且D的坐标(0,1).
P,且D的坐标(0,1). (1997•武汉)已知:如图,⊙M交x轴正半轴于A(x1,0)、B(x2,0)(x1<x2)两点,交y轴正半轴于C(0,y1)、D(0,y2)(y1<y2)两点.
(1997•武汉)已知:如图,⊙M交x轴正半轴于A(x1,0)、B(x2,0)(x1<x2)两点,交y轴正半轴于C(0,y1)、D(0,y2)(y1<y2)两点.