题目内容
已知,如图:⊙M交x轴于A(-| 3 |
| 3 |
 ,D两点.
,D两点.(1)求M点的坐标;
(2)P为弧BC上一动点,连接BC,PA,PC,当P点在弧BC上运动时.求证PC+PB=PA.
分析:(1)连接BD,由点A,B,C点的坐标,依据垂径定理,推出CD⊥AB,OA=OB,再根据勾股定理推出BC的长度,即可求出∠BCO的度数,然后根据圆周角定理推出∠CBD=90°,求得∠DBO=30°,再根据30°角的正切值推出OD的长度,即可推出OM的长度;
(2)在PA上截取PE=PB,连接AC,根据(1)中所推出的结论,首先求出△PMB和△ABC为等边三角形,然后通过求证△CPB和△AMB全等,即可推出AE=PC,最后通过等量代换即可推出结论.
(2)在PA上截取PE=PB,连接AC,根据(1)中所推出的结论,首先求出△PMB和△ABC为等边三角形,然后通过求证△CPB和△AMB全等,即可推出AE=PC,最后通过等量代换即可推出结论.
解答:解:(1)连接BD,
∵CD⊥AB,B(
,0),C(3,0),
∴BC=2
,
∴∠OCB=30°,
∵CD为直径,
∴∠CBD=90°,
∴∠OBD=30°,
∴tan30°=
=
,
∴OD=1,
∴OM=
-OD=1,
∴M点的坐标为(0,1),
(2)在PA上截取PE=PB,连接AC,
∵CD⊥AB,CD为直径,
∴OA=OB,
=
,
∴∠APB=2∠DCB,AC=BC,
∵∠DCB=30°,
∴∠APB=60°,∠CBA=60°,
∴∠CPA=60°,
∵PB=PE,
∴△PMB和△ABC为等边三角形,
∴∠AEB=120°,∠CPB=120°,BC=BA,
∵在△CPB和△AEB中,
,
∴△CPB≌△AEB(AAS),
∴AE=PC,
∵PA=EA+EP,
∴PA=PC+PB.
∵CD⊥AB,B(
| 3 |
∴BC=2
| 3 |
∴∠OCB=30°,
∵CD为直径,
∴∠CBD=90°,
∴∠OBD=30°,
∴tan30°=
| OD |
| OB |
| ||
| 3 |
∴OD=1,
∴OM=
| CD |
| 2 |
∴M点的坐标为(0,1),

(2)在PA上截取PE=PB,连接AC,
∵CD⊥AB,CD为直径,
∴OA=OB,
 |
| AD |
 |
| BD |
∴∠APB=2∠DCB,AC=BC,
∵∠DCB=30°,
∴∠APB=60°,∠CBA=60°,
∴∠CPA=60°,
∵PB=PE,
∴△PMB和△ABC为等边三角形,
∴∠AEB=120°,∠CPB=120°,BC=BA,
∵在△CPB和△AEB中,
|
∴△CPB≌△AEB(AAS),
∴AE=PC,
∵PA=EA+EP,
∴PA=PC+PB.
点评:本题主要考查圆周角定理、全等三角形的判定与性质、勾股定理、锐角三角函数的定义、垂径定理,关键在于正确地作出辅助线,熟练运用相关的性质定理求出相关角的度数、角的相等关系、线段的相等关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
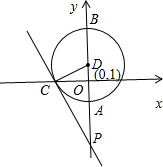 已知,如图,⊙D交y轴于A、B,交x轴于C,过C的直线:y=-2
已知,如图,⊙D交y轴于A、B,交x轴于C,过C的直线:y=-2 P,且D的坐标(0,1).
P,且D的坐标(0,1). (1997•武汉)已知:如图,⊙M交x轴正半轴于A(x1,0)、B(x2,0)(x1<x2)两点,交y轴正半轴于C(0,y1)、D(0,y2)(y1<y2)两点.
(1997•武汉)已知:如图,⊙M交x轴正半轴于A(x1,0)、B(x2,0)(x1<x2)两点,交y轴正半轴于C(0,y1)、D(0,y2)(y1<y2)两点.