题目内容
18.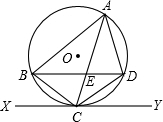 如图,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC,BD相交于点E.
如图,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC,BD相交于点E.(1)求证:△ABE≌△ACD;
(2)若AB=6cm,BC=4cm,ED=2cm,求AE的长.
分析 (1)连结OC,如图,先根据切线的性质得OC⊥XY,由于BD∥XY,则OC⊥BD,则利用垂径定理可得$\widehat{BC}$=$\widehat{CD}$,接着根据圆周角定理得∠1=∠2,且∠3=∠4,于是可根据“ASA”判断△ABE≌△ACD;
(2)由$\widehat{BC}$=$\widehat{CD}$得BC=CD=4,再由∠5=∠2,∠4公共可判断△CDE∽△CAD,利用相似比可计算出CE=$\frac{8}{3}$,然后计算AC-CE即可得到AE的长.
解答  (1)证明:连结OC,如图,
(1)证明:连结OC,如图,
∵直线XY切⊙O于点C,
∴OC⊥XY,
∵BD∥XY,
∴OC⊥BD,
∴$\widehat{BC}$=$\widehat{CD}$,
∴∠1=∠2,
在△ABE和△ACD中
$\left\{\begin{array}{l}{∠1=∠2}\\{AB=AC}\\{∠3=∠4}\end{array}\right.$,
∴△ABE≌△ACD;
(2)解:∵AB=AC,
∴AC=6,
∵$\widehat{BC}$=$\widehat{CD}$,
∴BC=CD=4,∠5=∠2,
而∠4公共,
∴△CDE∽△CAD,
∴$\frac{CD}{AC}$=$\frac{CE}{CD}$,即$\frac{4}{6}$=$\frac{CE}{4}$,解得CE=$\frac{8}{3}$,
∴AE=AC-CE=6-$\frac{8}{3}$=$\frac{10}{3}$(cm).
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理、全等三角形的判定与性质和三角形相似的判定与性质.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.当a、b满足什么条件时,方程(2b2-18)x=3与方程组$\left\{\begin{array}{l}{ax-y=1}\\{3x-2y=b-5}\end{array}\right.$都无解.
8.在△ABC中,BC边上的高AH一定满足( )
| A. | 在△ABC的内部 | B. | AH≤AB | C. | AH≤BH | D. | ∠AHC=90° |
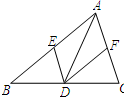 如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F,若添加条件∠BAC=90°,则四边形AEDF是矩形;若添加条件AD平分∠BAC,则四边形AEDF是菱形;若添加条件∠BAC=90°且AD平分∠BAC,则四边形AEDF是正方形.
如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F,若添加条件∠BAC=90°,则四边形AEDF是矩形;若添加条件AD平分∠BAC,则四边形AEDF是菱形;若添加条件∠BAC=90°且AD平分∠BAC,则四边形AEDF是正方形.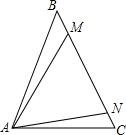 如图,在已知△ABC中,AB=AC,MN=NA,∠BAM=∠NAC,则∠MAN=60°.
如图,在已知△ABC中,AB=AC,MN=NA,∠BAM=∠NAC,则∠MAN=60°.