题目内容
边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点 E在第一象限，且DE⊥DC，DE＝DC. 以直线AB为对称轴的抛物线过
C，E两点.
（1）求抛物线的解析式；
（2）点P从点C出发，沿射线CB以每秒1个单位长度的速度运动，运动时间为t秒.
过点P作PF⊥CD于点F. 当t为何值时，以点P，F，D为顶点的三角形与△COD
相似？
（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以
点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的
点的坐标；若不存在，请说明理由.
 |
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
≈1.73）
的解是 .
的度数是（ ）
如图1，对于平面上小于等于
的
，我们给出如下定义：若点P在
的内部或边上，作
于点E，
于点
，则将
称为点
P与的“点角距”，记作d(∠MON，P)．如图2，在平面直角坐标系xoy中，
x、y正半轴所组成的角为∠xOy．
 |
（1）已知点A（5，0）、点B（3，2），则d(∠xOy，A) ＝ ，d(∠xOy，B) ＝ ．
（2）若点P为∠xOy内部或边上的动点，且满足d(∠xOy，P)＝5，画出点P运动所
形成的图形．
（3）如图3与图4，在平面直角坐标系xoy中，射线OT的函数关系式为y＝
x（x≥0）．
①在图3中，点C的坐标为（4，1），试求d(∠xOT，C)的值；
②在图4中，抛物线y＝－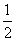
x 2＋2x＋
经过A（5，0）与点D(3，4)两点，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求当d(∠xOT，Q)取最大值时点Q 的坐标．
则∠2－∠3＝ °．