题目内容
 如图,一艘船每小时35海里的速度向东北方向(北偏东45°)航行,在A处观测灯塔C在船的北偏东74°方向,航行了12分钟后到达B处,这时灯塔C恰好在船的正东方向,已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗,为什么?(参考数据:tan29°≈0.50,sin29°≈0.48,cos29°≈0.87)
如图,一艘船每小时35海里的速度向东北方向(北偏东45°)航行,在A处观测灯塔C在船的北偏东74°方向,航行了12分钟后到达B处,这时灯塔C恰好在船的正东方向,已知距离此灯塔8海里以外的海区为航行安全区域,这艘船可以继续沿东北方向航行吗,为什么?(参考数据:tan29°≈0.50,sin29°≈0.48,cos29°≈0.87)考点:解直角三角形的应用-方向角问题
专题:
分析:问这艘船能否可以继续沿东北方向航行,只要求出C到AB的距离CD,再将CD与8海里比较即可.可以作与正北方向平行的直线,与CB的延长线相交于点E.则△ABE,△ACE都是直角三角形,可以运用勾股定理来计算.
解答: 解:作与正北方向平行的直线,与CB的延长线相交于点E,过点C作CD⊥AB于D.
解:作与正北方向平行的直线,与CB的延长线相交于点E,过点C作CD⊥AB于D.
∵AB=35×
=7(海里),
∵∠EAB=45°,∠AEB=90°,
∴AE=BE=AB•sin45°=7×
=
(海里),
∵∠CAE=74°,∠ACS=90°,
∴EC=AE•tan74°≈
×3.49≈17.27(海里),
∴BC=EC-BE≈12.32(海里),
∵∠DBC=∠ABE=45°,
∴CD=BC•sin45°≈12.32×
≈8.71>8,
∴这艘船可以继续沿东北方向航行.
 解:作与正北方向平行的直线,与CB的延长线相交于点E,过点C作CD⊥AB于D.
解:作与正北方向平行的直线,与CB的延长线相交于点E,过点C作CD⊥AB于D.∵AB=35×
| 12 |
| 60 |
∵∠EAB=45°,∠AEB=90°,
∴AE=BE=AB•sin45°=7×
| ||
| 2 |
7
| ||
| 2 |
∵∠CAE=74°,∠ACS=90°,
∴EC=AE•tan74°≈
7
| ||
| 2 |
∴BC=EC-BE≈12.32(海里),
∵∠DBC=∠ABE=45°,
∴CD=BC•sin45°≈12.32×
| ||
| 2 |
∴这艘船可以继续沿东北方向航行.
点评:此题考查了解直角三角形的应用-方向角问题.此题难度适中,注意掌握辅助线的作法,注意能借助于方向角构造直角三角形并解此直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
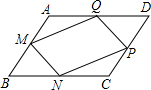 已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.
已知,如图,在?ABCD中,M、N、P、Q分别为AB、BC、CD、DA上的点,且AM=CP,BN=DQ,求证:MN∥QP.