题目内容
12.已知关于x的方程(k-1)x2+2x-5=0有两个实数根a、b.(1)求k的取值范围;
(2)若k是满足条件的最小整数,求a2+5ab+2a的值.
分析 (1)根据题意方程有两个实数根,则△≥0且k-1≠0,据此求出k的取值范围;
(2)首先求出k的最小整数,然后利用根与系数的关系求出代数式的值.
解答 解:(1)∵关于x的方程(k-1)x2+2x-5=0有两个实数根,
∴△≥0且k-1≠0,即4+20(k-1)≥0且k-1≠0,
∴k≥$\frac{4}{5}$且k≠1;
(2)∵k是满足条件的整数,
∴k=2,
∵a、b是方程x2+2x-5=0的两个实数根,
∴a2+2a-5=0,ab=-5,
∴a2+2a=5,
∴a2+5ab+2a=5+5×(-5)=-20.
点评 本题主要考查了根的判别式的知识,解答本题的关键是根据根的判别式的意义求出k的取值范围,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列等式成立的是( )
| A. | $\frac{1}{a}$+$\frac{2}{b}$=$\frac{3}{a+b}$ | B. | $\frac{a}{-a+b}=-\frac{a}{a+b}$ | C. | $\frac{ab}{ab-{b}^{2}}=\frac{a}{a-b}$ | D. | $\frac{2}{2a+b}=\frac{1}{a+b}$ |
2.七边形的外角和为( )
| A. | 1260° | B. | 900° | C. | 360° | D. | 180° |
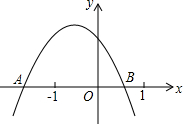 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,图象与x轴交于A(x1,0)B(x2,0)两点,点M(x0,y0)是图象上另一点,且x0>1.现有以下结论:①abc>0;②b<2a;③a+b+c>0;④a(x0-x1)(x0-x2)<0.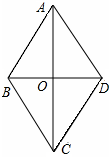 已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( )
已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( ) 如图,AO=CO,BO=DO,求证:AD=BC,AD∥BC.
如图,AO=CO,BO=DO,求证:AD=BC,AD∥BC.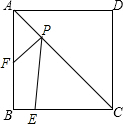 如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为$\sqrt{17}$.
如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为$\sqrt{17}$.