题目内容
1.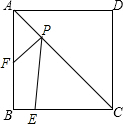 如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为$\sqrt{17}$.
如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB上的一点,AF=2,P为AC上一个动点,则PF+PE的最小值为$\sqrt{17}$.
分析 作E关于直线AC的对称点E′,连接E′F,则E′F即为所求,过F作FG⊥CD于G,在Rt△E′FG中,利用勾股定理即可求出E′F的长.
解答 解:作E关于直线AC的对称点E′,连接E′F,则E′F即为所求,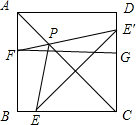
过F作FG⊥CD于G,
在Rt△E′FG中,
GE′=CD-BE-BF=4-1-2=1,GF=4,
所以E′F=$\sqrt{F{G}^{2}+E′{G}^{2}}$=$\sqrt{17}$.
故答案为:$\sqrt{17}$.
点评 本题考查的是最短线路问题,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
相关题目
9.已知a,b互为倒数,|c-1|=2,则abc的值为( )
| A. | -1或3 | B. | -1 | C. | 3 | D. | ±2 |
10.下列方程中没有实数根的是( )
| A. | x2-x-1=0 | B. | x2+3x+2=0 | C. | 2015x2+11x-20=0 | D. | x2+x+2=0 |
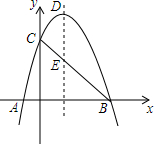 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.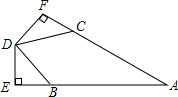 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,
已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,