题目内容
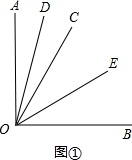
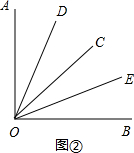
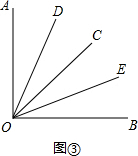
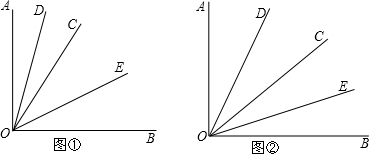
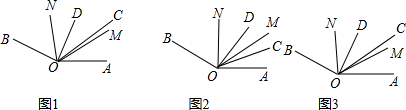
 如图,OD,OC分别是∠AOB和∠EOF的角平分线,∠AOB=∠EOF.
如图,OD,OC分别是∠AOB和∠EOF的角平分线,∠AOB=∠EOF.
(1)若∠DOC是直角,那么图中还有∠________和∠________也是直角.
(2)∠DOC=50°,∠BOF=140°,求∠DOC的大小.
(3)有人说,∠DOC的度数是∠AOE和∠BOF的平均数,你同意吗?说出理由.
解:(1)∵OD,OC分别是∠AOB和∠EOF的角平分线,
∴∠BOD=∠AOD,∠COE=∠COF,
∵∠AOB=∠EOF,
∴∠BOD=∠AOD=∠COE=∠COF,
∵∠DOC=90°=∠AOE+∠AOD+∠COE,
∴∠BOE=∠AOE+∠AOD+∠BOD=90°,
同理∠AOF=90°,
故答案为:BOE,FOA.
(2)∠DOC=50°.
(3)∠DOC的度数是∠AOE和∠BOF的平均数,
理由是:∵∠DOC=∠AOE+∠AOD+∠COE,
 (∠AOE+∠BOF)=
(∠AOE+∠BOF)= (∠AOE+∠AOE+∠AOD+∠BOD+∠EOC+∠FOC)=∠AOE+∠AOD+∠COE,
(∠AOE+∠AOE+∠AOD+∠BOD+∠EOC+∠FOC)=∠AOE+∠AOD+∠COE,
∴∠DOC= (∠AOE+∠BOF),
(∠AOE+∠BOF),
即:∠DOC的度数是∠AOE和∠BOF的平均数.
分析:(1)根据角平分线定义求出∠BOD=∠AOD=∠COE=∠COF即可;
(2)根据已知条件写出即可;
(3)根据(1)和角的大小关系求出即可.
点评:本题主要考查对角的大小计算,角平分线的定义等知识点的理解和掌握,能灵活地运用性质进行推理是解此题的关键.
∴∠BOD=∠AOD,∠COE=∠COF,
∵∠AOB=∠EOF,
∴∠BOD=∠AOD=∠COE=∠COF,
∵∠DOC=90°=∠AOE+∠AOD+∠COE,
∴∠BOE=∠AOE+∠AOD+∠BOD=90°,
同理∠AOF=90°,
故答案为:BOE,FOA.
(2)∠DOC=50°.
(3)∠DOC的度数是∠AOE和∠BOF的平均数,
理由是:∵∠DOC=∠AOE+∠AOD+∠COE,
 (∠AOE+∠BOF)=
(∠AOE+∠BOF)= (∠AOE+∠AOE+∠AOD+∠BOD+∠EOC+∠FOC)=∠AOE+∠AOD+∠COE,
(∠AOE+∠AOE+∠AOD+∠BOD+∠EOC+∠FOC)=∠AOE+∠AOD+∠COE,∴∠DOC=
 (∠AOE+∠BOF),
(∠AOE+∠BOF),即:∠DOC的度数是∠AOE和∠BOF的平均数.
分析:(1)根据角平分线定义求出∠BOD=∠AOD=∠COE=∠COF即可;
(2)根据已知条件写出即可;
(3)根据(1)和角的大小关系求出即可.
点评:本题主要考查对角的大小计算,角平分线的定义等知识点的理解和掌握,能灵活地运用性质进行推理是解此题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
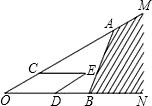 如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=
如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=