题目内容
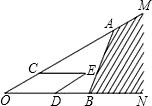 如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=
如图,点A,B分别在射线OM,ON上,C,D分别是线段OA和OB上的点,以OC,OD为邻边作平行四边形OCED,下面给出三种作法的条件:①取OC=| 3 |
| 4 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 5 |
| A、① | B、①② | C、①②③ | D、②③ |
分析:根据平行四边形的性质和三角形相似的性质,然后逐个验证相似比即可得出答案.
解答:解:OA=a,OB=b,若使点E落在阴影部分则△ACE∽△AOB,△BED∽△BAO,只要验证答案中的条件符合三角形的相似比即可.
①取OC=
OA,OD=
OB,即OC=
,OD=
,
∴
=
,
∵OC=
,
∴AC=
a,解得CE=
b,CE=OD=
OB=
b,
∴能使点E落在阴影区域内,
故①正确;
②当OC=
OA,OD=
OB时,即OC=
,OD=
,
∴
=
,
∵OC=
解得CE=
b,与OD=CE=
相矛盾,错误.同理③也错误.
故选A.
①取OC=
| 3 |
| 4 |
| 3 |
| 5 |
| 3a |
| 4 |
| 3b |
| 5 |
∴
| AC |
| OA |
| CE |
| OB |

∵OC=
| 3a |
| 4 |
∴AC=
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
∴能使点E落在阴影区域内,
故①正确;
②当OC=
| 1 |
| 2 |
| 1 |
| 3 |
| a |
| 2 |
| b |
| 3 |
∴
| AC |
| OA |
| CE |
| OB |
∵OC=
| a |
| 2 |
| 1 |
| 2 |
| b |
| 3 |
故选A.
点评:解答此题的关键是熟知平行四边形的性质,即三角形相似的性质,两三角形相似其相似比等于各边的比的值.

练习册系列答案
相关题目
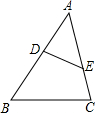 如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为
如图,点D、E分别在△ABC的边上AB、AC上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE的长为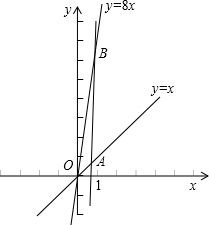 如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当
如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当 19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数.
19、如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数. 12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
12、如图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( ) 如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.
如图,点A、B分别在直线l1、l2上,过点A作到l2的距离AM,过点B作直线l3∥l1.