题目内容
 一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB.
一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB.求:
(1)这两个函数的表达式;
(2)△AOB的面积S.
分析:(1)先根据待定系数法确定正比例函数解析式为y=
x;再利用两点间的距离公式计算出OA=5,则B点坐标为(0,-5),然后根据待定系数法确定直线AB的解析式;
(2)根据三角形面积公式求解.
| 4 |
| 3 |
(2)根据三角形面积公式求解.
解答:解:(1)设直线OA的解析式为y=kx,
把A(3,4)代入得4=3k,解得k=
,
所以直线OA的解析式为y=
x;
∵A点坐标为(3,4),
∴OA=
=5,
∴OB=OA=5,
∴B点坐标为(0,-5),
设直线AB的解析式为y=ax+b,
把A(3,4)、B(0,-5)代入得
,解得
,
∴直线AB的解析式为y=3x-5;
(2)△AOB的面积S=
×5×3=
.
把A(3,4)代入得4=3k,解得k=
| 4 |
| 3 |
所以直线OA的解析式为y=
| 4 |
| 3 |
∵A点坐标为(3,4),
∴OA=
| 32+42 |
∴OB=OA=5,
∴B点坐标为(0,-5),
设直线AB的解析式为y=ax+b,
把A(3,4)、B(0,-5)代入得
|
|
∴直线AB的解析式为y=3x-5;
(2)△AOB的面积S=
| 1 |
| 2 |
| 15 |
| 2 |
点评:本题考查了两条直线相交或平行问题:若直线y=k1x+b1与直线y=k2x+b2平行,则k1=k2;若直线y=k1x+b1与直线y=k2x+b2相交,则由两解析式所组成的方程组的解为交点坐标.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
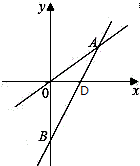 如图,表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式及两直线与x轴围成三角形的面积.
如图,表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式及两直线与x轴围成三角形的面积. 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.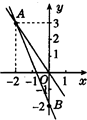 如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.
如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.