题目内容
6. 如图,正方形ABCD和正三角形AEF都内接于⊙O,则$\frac{{S}_{△AEF}}{{S}_{正方形ABCD}}$=$\frac{3\sqrt{3}}{8}$.
如图,正方形ABCD和正三角形AEF都内接于⊙O,则$\frac{{S}_{△AEF}}{{S}_{正方形ABCD}}$=$\frac{3\sqrt{3}}{8}$.
分析 连接OB、OE,过点O作OH⊥AE,OG⊥AB,可得到△OBG为等腰直角三角形,△OEH为含30°的直角三角形,设⊙O的半径为r,可求得BG=OG=$\frac{\sqrt{2}}{2}$r,HE=$\frac{\sqrt{3}}{2}$r,OH=$\frac{1}{2}$r,于是可求得三角形和正方形的面积,最后可求得它们的面积比.
解答 解:如图所示:连接OB、OE,过点O作OH⊥AE,OG⊥AB.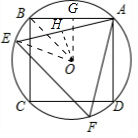
设⊙O的半径为r.
∵ABCD为⊙O的内接正方形,
∴GO=BG=$\frac{\sqrt{2}}{2}$r.
∴正方形ABCD的面积=8×$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$r×$\frac{\sqrt{2}}{2}$r=2r2.
∵△AEF为⊙的内接正三角形,
∴EH=$\frac{\sqrt{3}}{2}$r,OH=$\frac{1}{2}$r.
∴△AEF的面积=6×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$r×$\frac{1}{2}$r=$\frac{3\sqrt{3}}{4}$r2.
∴$\frac{{S}_{△AEF}}{{S}_{正方形ABCD}}$=$\frac{3\sqrt{3}}{8}$.
故答案为:$\frac{3\sqrt{3}}{8}$.
点评 本题主要考查的是正多边形和圆,掌握此类问题的辅助线的作法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.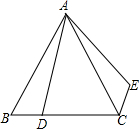 如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
 如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )
如图,△ABC是等边三角形,D为BC边上的点,△ABD绕点A沿逆时针方向旋转后到达△ACE的位置,那么旋转了( )| A. | 75° | B. | 60° | C. | 45° | D. | 15° |
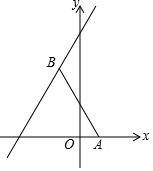 如图,点A的坐标为(2,0),点B在直线y=$\frac{4}{3}$x+4上运动,当线段AB最短时,AB的长度为4.
如图,点A的坐标为(2,0),点B在直线y=$\frac{4}{3}$x+4上运动,当线段AB最短时,AB的长度为4.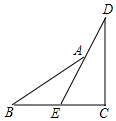 如图,阅读下面的题目及分析过程,并按要求进行证明.
如图,阅读下面的题目及分析过程,并按要求进行证明.