题目内容
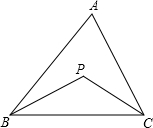
如图，BP、CP分别是△ABC的角平分线，∠A=80°，那么∠BPC=________°．
130
分析：在△ABC中，根据角平分线的定义及三角形内角和定理，先求得∠ABC+∠ACB的值，从而求得∠CBP+∠PCB的值；然后在
△BPC中利用三角形内角和定理求得∠BPC度数．
解答：∵BP、CP分别是△ABC的角平分线
∴∠ABP=∠CBP，∠ACP=∠PCB；
∵∠A+∠ABC+∠ACB=180°，
∴∠A+2∠CBP+2∠PCB=180°；
∵∠A=80°，
∴∠CBP+∠PCB=50°；
在△BPC中，
又∵∠BPC+∠CBP+∠PCB=180°，
∴∠BPC=130°．
故答案为：130°．
点评：本题考查三角形的内角和定力及角平分线的性质，解答本题时要灵活运用所学的知识．
分析：在△ABC中，根据角平分线的定义及三角形内角和定理，先求得∠ABC+∠ACB的值，从而求得∠CBP+∠PCB的值；然后在
△BPC中利用三角形内角和定理求得∠BPC度数．
解答：∵BP、CP分别是△ABC的角平分线
∴∠ABP=∠CBP，∠ACP=∠PCB；
∵∠A+∠ABC+∠ACB=180°，
∴∠A+2∠CBP+2∠PCB=180°；
∵∠A=80°，
∴∠CBP+∠PCB=50°；
在△BPC中，
又∵∠BPC+∠CBP+∠PCB=180°，
∴∠BPC=130°．
故答案为：130°．
点评：本题考查三角形的内角和定力及角平分线的性质，解答本题时要灵活运用所学的知识．
练习册系列答案
相关题目
如图BP、CP分别平分∠ABC、∠ACB，请你探索∠A和∠P的数量关系．
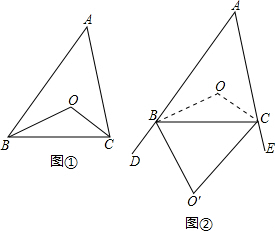
∠A（不必证明，本题可直接运用）；在图②中，当BO′、CO′分别为∠ABC和∠ACB的外角平分线时，求∠BO′C与∠A的数量关系．我们可以利用“转化”的思想，将未知的∠BO′C转化为已知的∠BOC：如图②，作BO、CO平分∠ABC和∠ACB．
