题目内容
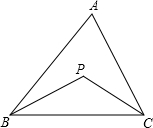 如图BP、CP分别平分∠ABC、∠ACB,请你探索∠A和∠P的数量关系.
如图BP、CP分别平分∠ABC、∠ACB,请你探索∠A和∠P的数量关系.解:∵BP平分∠ABC(已知)
∴∠PBC=
| 1 |
| 2 |
角平分线的定义
角平分线的定义
).同理可得∠PCB=
| 1 |
| 2 |
∵∠BPC+∠PBC+∠PCB=180°(
三角形的内角和等于180°
三角形的内角和等于180°
)∴∠BPC=180°-∠PBC-∠PCB (等式的性质)
=180°-
| 1 |
| 2 |
等量代换
等量代换
)=180°-
| 1 |
| 2 |
A
A
)=90°+
| 1 |
| 2 |
A
A
.分析:根据角平分线的定义、△BPC的内角和定理求得求得∠BPC=180°-∠PBC-∠PCB=180°-
(∠ABC+∠ACB )=90°+
∠A.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵BP平分∠ABC(已知)
∴∠PBC=
∠ABC(角平分线的定义).
同理可得∠PCB=
∠ACB
∵∠BPC+∠PBC+∠PCB=180°(三角形的内角和等于180°)
∴∠BPC=180°-∠PBC-∠PCB(等式的性质)
=180°-
(∠ABC+∠ACB )(等量代换)
=180°-
(180°-∠A)
=90°+
∠A.
故答案是:角平分线的定义;三角形的内角和等于180°;等量代换;A;A.
∴∠PBC=
| 1 |
| 2 |
同理可得∠PCB=
| 1 |
| 2 |
∵∠BPC+∠PBC+∠PCB=180°(三角形的内角和等于180°)
∴∠BPC=180°-∠PBC-∠PCB(等式的性质)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
故答案是:角平分线的定义;三角形的内角和等于180°;等量代换;A;A.
点评:本题考查了三角形内角和定理、角平分线的定义.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
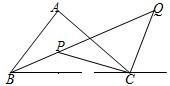 7、如图,在△ABC中,∠BAC=90°,BP、CP分别平分∠ABC、∠ACB,CQ是∠ACB的外角平分线,有下列结论①∠BPC=135°②∠PCQ=90°③∠Q=45°④△PCQ是等腰直角三角形,其中正确的结论有( )
7、如图,在△ABC中,∠BAC=90°,BP、CP分别平分∠ABC、∠ACB,CQ是∠ACB的外角平分线,有下列结论①∠BPC=135°②∠PCQ=90°③∠Q=45°④△PCQ是等腰直角三角形,其中正确的结论有( )
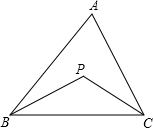 如图BP、CP分别平分∠ABC、∠ACB,请你探索∠A和∠P的数量关系.
如图BP、CP分别平分∠ABC、∠ACB,请你探索∠A和∠P的数量关系. ∠ABC (________).
∠ABC (________).