题目内容
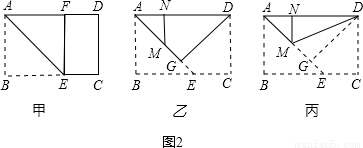
探索下列∠A与∠P之间的关系,并说明理由.
(1)如图①,BP、CP分别平分∠ABC、∠ACB;
(2)如图②,BP、CP分别平分∠ABC、∠ACB的补角:
(3)如图③,BP平分∠ABC的补角、CP平分∠ACB的补角.
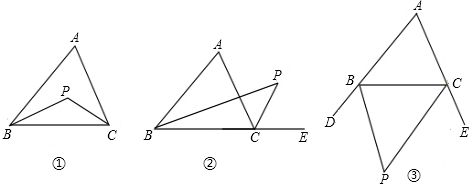
(1)如图①,BP、CP分别平分∠ABC、∠ACB;
(2)如图②,BP、CP分别平分∠ABC、∠ACB的补角:
(3)如图③,BP平分∠ABC的补角、CP平分∠ACB的补角.

分析:(1)根据BP、CP分别平分∠ABC和∠ACB,得到∠PBC=
∠ABC,∠PCB=
∠ACB,求出∠PBC+∠PCB,根据三角形的内角和定理求出∠P即可;
(2)根据∠ACE=∠A+∠ABC,和CP平分∠ACD,BP平分∠ABC,得到∠PBC=
∠ABC,∠PCA=
∠ACE=
∠A+
∠ABC,根据∠P=180°-(∠PBC+∠PCA+∠ACB),得到
∠A即可;
(3)根据∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,求出∠DBC+∠ECB,根据BP、CP分别平分∠DBC和∠ECD,得到∠PBC=
∠DBC,∠PCB=
∠ECB,求出∠PBC+∠PCB,即可求出答案.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据∠ACE=∠A+∠ABC,和CP平分∠ACD,BP平分∠ABC,得到∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,求出∠DBC+∠ECB,根据BP、CP分别平分∠DBC和∠ECD,得到∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵BP、CP分别平分∠ABC和∠ACB,
∴∠PBC=
∠ABC,∠PCB=
∠ACB,
∴∠PBC+∠PCB=
(∠ABC+∠ACB)=
×(180°-∠A),
∴∠P=180°-(∠PCB+∠PBC)=90°+
∠A.
(2)∠ACE=∠A+∠ABC,
∵CP平分∠ACE,BP平分∠ABC,
∴∠PBC=
∠ABC,∠PCA=
∠ACE=
∠A+
∠ABC,
∴∠P=180°-(∠PBC+∠PCA+∠ACB)=
∠A;
(3)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC,
∵BP、CP分别平分∠DBC和∠ECD,
∴∠PBC=
∠DBC,∠PCB=
∠ECB,
∴∠PBC+∠PCB=
(∠DBC+∠ECB),
∴∠P=180°-(∠PBC+∠PCB)=180°-
(∠DBC+∠ECB)=90°-
∠A.
故答案为:(1)∠P=90°+
∠A;(2)∠P=∠A;(3)∠P=90°-
∠A,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠P=180°-(∠PCB+∠PBC)=90°+
| 1 |
| 2 |
(2)∠ACE=∠A+∠ABC,
∵CP平分∠ACE,BP平分∠ABC,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠P=180°-(∠PBC+∠PCA+∠ACB)=
| 1 |
| 2 |
(3)∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC,
∵BP、CP分别平分∠DBC和∠ECD,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBC+∠PCB=
| 1 |
| 2 |
∴∠P=180°-(∠PBC+∠PCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(1)∠P=90°+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查对三角形的内角和定理,三角形的外角,角平分线的定义等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目



 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题:


 的矩形纸片称为标准纸.请解决下列问题:
的矩形纸片称为标准纸.请解决下列问题:


 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题: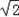 ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.…
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.…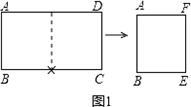
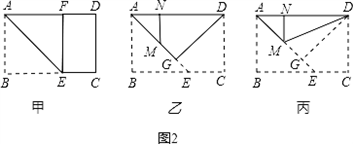
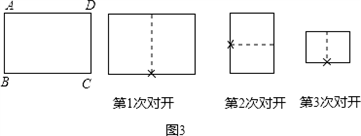
 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题: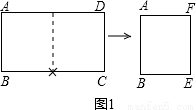
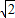 ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.