题目内容
5.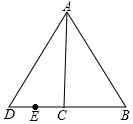 如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.
如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.(1)求证:△ABD是等边三角形;
(2)若E为线段CD的中点,且AD=4,点P为线段AC上一动点,连接EP,BP.
①求EP+$\frac{1}{2}$AP的最小值;
②求2BP+AP的最小值.
分析 (1)根据线段的垂直平分线的性质定理,可得AD=AB,只要证明∠B=60°即可解决问题.
(2)①如图1中,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′.由∠PAF=30°,∠PFA=90°,推出PF=$\frac{1}{2}$PA,推出PE+$\frac{1}{2}$PA=PE+PF,所以当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,求出EF′即可解决问题.
②如图2中,作PF⊥AD于F,EF′⊥AD于F′,交AC于P′.由∠PAF=30°,∠PFA=90°,推出PF=$\frac{1}{2}$PA,推出2BP+AP=2(PB+$\frac{1}{2}$PA)=2(PB+PF),所以当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,求出BF′即可解决问题.
解答 (1)证明:∵∠ACB=90°,∠BAC=30°
∴AC⊥BD,∠B=60°
∵DC=CB,
∴AD=AB,∵∠B=60°,
∴△ABD是等边三角形.
(2)①如图1中,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′.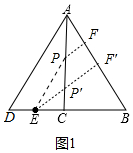
∵∠PAF=30°,∠PFA=90°,
∴PF=$\frac{1}{2}$PA,
∴PE+$\frac{1}{2}$PA=PE+PF,
∴当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,
在Rt△EF′B中,∵∠B=60°,EB=3,
∴EF′=EB•sin60°=$\frac{3\sqrt{3}}{2}$,
∴EP+$\frac{1}{2}$AP的最小值为$\frac{3\sqrt{3}}{2}$.
②如图2中,作PF⊥AD于F,EF′⊥AD于F′,交AC于P′.
∵∠PAF=30°,∠PFA=90°,
∴PF=$\frac{1}{2}$PA,
∴2BP+AP=2(PB+$\frac{1}{2}$PA)=2(PB+PF),
∴当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,
在Rt△DF′B中,∵∠D=60°,DB=4,
∴EF′=EB•sin60°=2$\sqrt{3}$,
∴2BP+AP的最小值为4$\sqrt{3}$.
点评 本题考查三角形综合题、等边三角形的判定和性质、直角三角形30度角性质、最短问题等知识,解题的关键是学会添加常用辅助线,利用垂线段最短解决最短问题,属于中考压轴题.

 如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.
如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.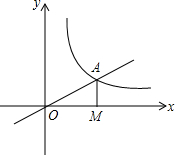 如图,正比例y=$\frac{1}{2}$x的图象与y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为及比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P坐标.
如图,正比例y=$\frac{1}{2}$x的图象与y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为及比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,P为x轴上一点,求使PA+PB的值最小时点P坐标.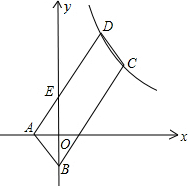 如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36.
如图,?ABCD的顶点A、B的坐标分别是A(-1,0),B(0,-3),顶点C、D在双曲线y=$\frac{k}{x}$上,边AD交y轴于点E,且?ABCD的面积是△ABE面积的8倍,则k=36.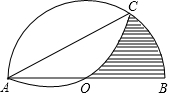 如图,AC是半圆O的一条弦,以弦AC为折线将弧AC折叠后过圆心O,⊙O的半径为2,则圆中阴影部分的面积为$\sqrt{3}$.
如图,AC是半圆O的一条弦,以弦AC为折线将弧AC折叠后过圆心O,⊙O的半径为2,则圆中阴影部分的面积为$\sqrt{3}$. 如图,在Rt△ABC中,∠ACB=90°,O是AB边上的一点,以OB为半径的⊙O与边AC相切于点E,与AB和BC交于点D、H.连接EH、DE,延长DE,BC交于点F.
如图,在Rt△ABC中,∠ACB=90°,O是AB边上的一点,以OB为半径的⊙O与边AC相切于点E,与AB和BC交于点D、H.连接EH、DE,延长DE,BC交于点F.