题目内容
20.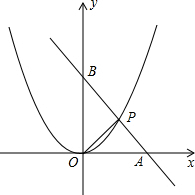 已知,如图,直线L经过A(6,0)和B(0,8)两点,它与抛物线y=ax2在第一象限内相交于点P,且△OAP是以AP为腰的等腰三角形,求a的值.
已知,如图,直线L经过A(6,0)和B(0,8)两点,它与抛物线y=ax2在第一象限内相交于点P,且△OAP是以AP为腰的等腰三角形,求a的值.
分析 首先求得直线AB的解析式,作PC⊥OA于C,然后等腰三角形的性质和平行线分线段成比例定理求得PC,从而求得点P的纵坐标,然后代入直线AB的解析式求得其横坐标,代入二次函数即可求解.
解答 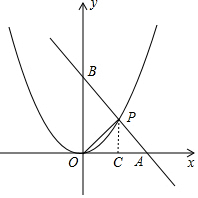 解:设直线AB的解析式为y=kx+b,
解:设直线AB的解析式为y=kx+b,
将A(6,0)和B(0,8)分别代入y=kx+b,
得k=-$\frac{4}{3}$,b=8,
故y=-$\frac{4}{3}$x+8,
∵△OAP是以AP为腰的等腰三角形,
①当AP=OP时:作PC⊥OA于C,
∴OC=OA,PC∥OB,
∴PC=$\frac{1}{2}$OB=4,
∴P的纵坐标为4,
把y=4代入y=-$\frac{4}{3}$x+8得,4=-$\frac{4}{3}$x+8,解得x=3,
∴P(3,4),
代入y=ax2得,4=9a,
∴a=$\frac{4}{9}$.
②当AP=OA时,
∵A(6,0),B(0,8),
∴OA=6,OB=8,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵PC∥OB,
∴$\frac{PA}{AB}$=$\frac{PC}{OB}$,即$\frac{6}{10}$=$\frac{PC}{8}$,
∴PC=4.8,
∴P的纵坐标为4.8,
把y=4.8代入y=-$\frac{4}{3}$x+8得,4.8=-$\frac{4}{3}$x+8,解得x=$\frac{12}{5}$,
∴P($\frac{12}{5}$,$\frac{24}{5}$),
代入y=ax2得,$\frac{24}{5}$=($\frac{12}{5}$)2a,
∴a=$\frac{5}{6}$.
综上,a的值为$\frac{4}{9}$或$\frac{5}{6}$.
点评 本题考查的是等腰三角形的性质,待定系数法求二次函数的解析式,二次函数的性质以及二次函数与图象相结合的应用,作出辅助线,关键三角形的中位线,从而求得P点的坐标是解题的关键.

| A. | 正数 | B. | 负数 | C. | 零 | D. | 任何有理数 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 南京 | 常州 | 苏州 | 上海 | |
| 到站时间 | 14:14 | 15:04 | 15:47 | |
| 发车时间 | 13:00 | 14:18 | 15:08 | |
| 里程/km | 0 | 138 | 219 | 303 |
(2)计算列车由南京驶往上海全程的平均速度.
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{6}$÷2=$\sqrt{3}$ | D. | $\sqrt{8}=4$ |