题目内容
【题目】阅读与理解:
如图1,直线![]() ,点P在a,b之间,M,N分别为a,b上的点,P,M,N三点不在同一直线上,PM与a的央角为
,点P在a,b之间,M,N分别为a,b上的点,P,M,N三点不在同一直线上,PM与a的央角为![]() ,PN与b的夹角为
,PN与b的夹角为![]() ,则
,则![]() .
.
理由如下:
过P点作直线![]() ,因为
,因为![]() ,所以
,所以![]() (如果两条直线都与第三条直线平行,那么这两条直线也互相平行).所以
(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).所以![]() ,
,![]() .(两直线平行,内错角相等),所以
.(两直线平行,内错角相等),所以![]() ,即
,即![]() .
.



计算与说明:
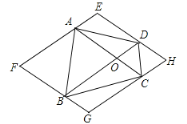
已知:如图2,AB与CD交于点O.
(1).若![]() ,求证:
,求证:![]() ;
;
(2)2.如图3,已知![]() ,AE平分
,AE平分![]() ,DE平分
,DE平分![]() .
.
①若![]() ,
,![]() ,请你求出
,请你求出![]() 的度数;
的度数;
②请问:图3中,![]() 与
与![]() 有怎样的数量关系?为什么?
有怎样的数量关系?为什么?
【答案】(1)证明见解析;(2). ![]() ;(3)
;(3)![]() .理由见解析
.理由见解析
【解析】
(1)根据平行线的判定与性质即可证明;(2)①过E点作FE∥AC,即FE∥AC∥BD,根据已知条件求出∠EDB与∠CAE,再根据阅读材料得出∠E=∠EDB+∠CAE,即可进行求解;②根据外角定理知∠BOC=∠BAC+∠C,由平行的性质得出∠E=∠EDB+∠CAE=![]() ∠CDB+
∠CDB+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ∠BOC.
∠BOC.
(1)∵![]() ,
,
∴AC∥BD,
∴![]()
(2)①∵![]() ,∴AC∥BD,
,∴AC∥BD,
过E点作FE∥AC,即FE∥AC∥BD,
∵AE平分![]() ,
,![]() ,∴∠CAE=
,∴∠CAE=![]()
![]() =25°,
=25°,
∵![]() ,∴∠CDB=60°,∵DE平分
,∴∠CDB=60°,∵DE平分![]() , ∴∠BDE=
, ∴∠BDE=![]()
![]() =30°,
=30°,
由阅读材料得∠E=∠EDB+∠CAE=25°+30°=55°;
②![]() ,理由如下:
,理由如下:
∵∠BOC是△ACO的一个外角
∴∠BOC=∠BAC+∠C,
∵ FE∥AC∥BD,
∴∠C=∠CDB
∴∠E=∠EDB+∠CAE=![]() ∠CDB+
∠CDB+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ∠BOC.
∠BOC.
即![]()


练习册系列答案
相关题目