题目内容
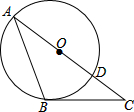 如图,△ABC中,BC=2,∠C=2∠A=45°,在AC边上取一点O,以点O为圆心,OA为半径的圆与AC边相交于点D,⊙O经过点B.
如图,△ABC中,BC=2,∠C=2∠A=45°,在AC边上取一点O,以点O为圆心,OA为半径的圆与AC边相交于点D,⊙O经过点B.(1)求证:BC是⊙O的切线;
(2)求CD的长.
考点:切线的判定
专题:证明题
分析:(1)连接OB,由OA=OB得∠A=∠OBA,根据三角形外角性质可得∠BOC=2∠A,由于∠C=2∠A=45°,所以∠BOC=45°,于是得到∠OBC=90°,则可根据切线的判定定理得到BC是⊙O的切线;
(2)由∠C=∠BOC=45°,可判断△OBC为等腰直角三角形,根据等腰直角三角形的性质得OB=BC=2,OC=
BC=2
,所以CD=OC-OD=2
-2.
(2)由∠C=∠BOC=45°,可判断△OBC为等腰直角三角形,根据等腰直角三角形的性质得OB=BC=2,OC=
| 2 |
| 2 |
| 2 |
解答: (1)证明:连接OB,如图,
(1)证明:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA,
∴∠BOC=∠A+∠OBA=2∠A,
而∠C=2∠A=45°,
∴∠BOC=45°,
∴∠OBC=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:∵∠C=∠BOC=45°,
∴△OBC为等腰直角三角形,
∴OB=BC=2,OC=
BC=2
,
∴CD=OC-OD=2
-2.
 (1)证明:连接OB,如图,
(1)证明:连接OB,如图,∵OA=OB,
∴∠A=∠OBA,
∴∠BOC=∠A+∠OBA=2∠A,
而∠C=2∠A=45°,
∴∠BOC=45°,
∴∠OBC=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:∵∠C=∠BOC=45°,
∴△OBC为等腰直角三角形,
∴OB=BC=2,OC=
| 2 |
| 2 |
∴CD=OC-OD=2
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了等腰直角三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 写出如图的符合下列条件的角.(图中所有的角均指小于平角的角).
写出如图的符合下列条件的角.(图中所有的角均指小于平角的角).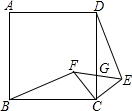 如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.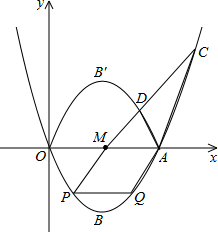 如图,已知二次函数的图象过点O(0,0),A(4,0),B(2,-
如图,已知二次函数的图象过点O(0,0),A(4,0),B(2,- 如图,用火柴棍连续搭建三角形和正方形,公共边只用一根火柴棍.如果搭建三角形和正方形共用了77根火柴棍,并且三角形的个数比正方形的个数少5个,那么一共能连续搭建三角形、正方形各多少个?
如图,用火柴棍连续搭建三角形和正方形,公共边只用一根火柴棍.如果搭建三角形和正方形共用了77根火柴棍,并且三角形的个数比正方形的个数少5个,那么一共能连续搭建三角形、正方形各多少个?