题目内容
4.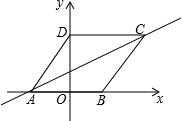 如图,在平面直角坐标系中,O为坐标原点,四边形ABCF是菱形,若点C的坐标为(5,4).则直线AC的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$.
如图,在平面直角坐标系中,O为坐标原点,四边形ABCF是菱形,若点C的坐标为(5,4).则直线AC的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$.
分析 根据菱形的性质得CD∥AB,CD=AD,则由C点坐标得到CD=5,OD=4,所以AD=5,在Rt△AOD中利用勾股定理计算出OA=3,则A(-3,0),然后利用待定系数法求直线AC的解析式.
解答 解:∵四边形ABCF是菱形,
∴CD∥AB,CD=AD,
∵点C的坐标为(5,4),
∴CD=5,OD=4,
∴AD=5,
在Rt△AOD中,OA=$\sqrt{A{D}^{2}-O{D}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴A(-3,0),
设直线AC的解析式为y=kx+b,
把A(-3,0),C(5,4)代入得$\left\{\begin{array}{l}{-3k+b=0}\\{5k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$.
故答案为y=$\frac{1}{2}$x+$\frac{3}{2}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了待定系数法求一次函数解析式.

练习册系列答案
相关题目
15.一个长方形在平面直角坐标系中,它的三个顶点的坐标分别为(-3,-1),(2,-1),(2,2),则第四个顶点的坐标为( )
| A. | (-3,2) | B. | (3,2) | C. | (-3,-4) | D. | (7,2) |
16.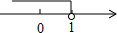 不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
 不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )| A. | a<1 | B. | a<2 | C. | a=1 | D. | a=2 |
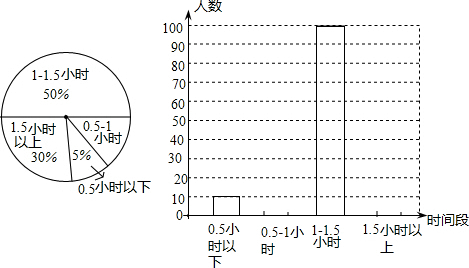
 某经销商批发了一批无锡水蜜桃,为了打开销路,对1200个水蜜桃进行打包优惠出售,打包方式及售价如图,假设用这两种打包方式恰好装完全部水蜜桃.
某经销商批发了一批无锡水蜜桃,为了打开销路,对1200个水蜜桃进行打包优惠出售,打包方式及售价如图,假设用这两种打包方式恰好装完全部水蜜桃.