题目内容
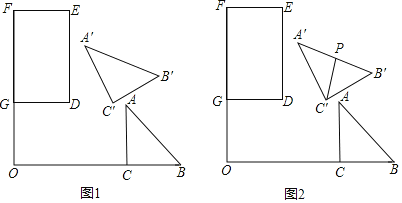
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
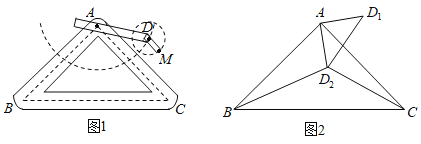
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)①![]() ,或
,或![]() ;②
;②![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)①分两种情形分别求解即可.
②显然∠MAD不能为直角.当∠AMD为直角时,根据AM2=AD2-DM2,计算即可,当∠ADM=90°时,根据AM2=AD2+DM2,计算即可.
(2)连接CD.首先利用勾股定理求出CD1,再利用全等三角形的性质证明BD2=CD1即可.
(1)①![]() ,或
,或![]() .
.
②显然![]() 不能为直角,
不能为直角,
当![]() 为直角时,
为直角时,
![]() ,∴
,∴![]() .
.
当![]() 为直角时,
为直角时,
![]() ,∴
,∴![]() .
.
(2)连结![]() ,
,
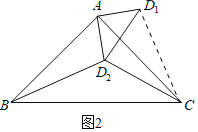
由题意得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
即![]() .
.
又∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目