Question

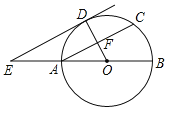
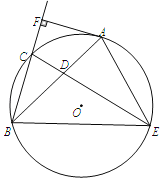
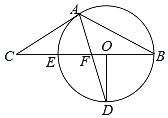
【题目】如图，在正方形中，、分别为、的中点，连接，交于点，将沿对折，得到，延长交延长线于点，下列4个结论：①；②；③；④；正确的结论有__________

Answer 1

【答案】①②③④

【解析】

①先根据正方形的性质、线段中点的定义可得，再根据三角形全等的判定定理与性质即可得；②先根据①中的全等三角形可得，再根据三角形的内角和定理、等量代换即可得；③设正方形的边长为，，再根据折叠的性质可得，然后根据平行线的性质、等腰三角形的性质可得，最后在中，利用勾股定理可求出x的值，由此利用正弦的定义即可得；④先利用勾股定理求出AE的长，再利用等面积法求出BG的长，然后利用勾股定理可得EG的长，最后分别求出与即可得．

四边形ABCD是正方形

点、分别为、的中点

在和中，

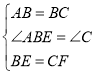
，则结论①正确

由①已证：

又

，则结论②正确

设正方形的边长为，

则

由折叠的性质得：

四边形ABCD是正方形

在中，，即

解得

，则结论③正确

在③假设的基础上可得：

又，即

，则结论④正确

综上，正确的结论有①②③④

故答案为：①②③④．