题目内容
6．抛物线y=x2+2x+m-1与x轴有两个不同的交点，则m的取值范围是m＜2．分析 利用判别式的意义得到△=22-4（m-1）＞0，然后解不等式即可．
解答 解：根据题意得△=22-4（m-1）＞0，
解得m＜2．
故答案为m＜2．
点评 本题考查了抛物线与x轴的交点：对于二次函数y=ax2+bx+c（a，b，c是常数，a≠0），△=b2-4ac决定抛物线与x轴的交点个数：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．
练习册系列答案
相关题目
在如图所示的方格纸中，按下列要求画图：
14．
如图，△ABC≌△ADE，若∠BAC=75°，∠E=40°，则∠B的度数为（ ）
如图，△ABC≌△ADE，若∠BAC=75°，∠E=40°，则∠B的度数为（ ）| A． | 75° | B． | 40° | C． | 65° | D． | 115° |
如图，将长和宽分别是a，b的长方形纸片的四个角都剪去一个边长为x的正方形．用含a，b，x的代数式表示纸片剩余部分的面积为ab-4x2．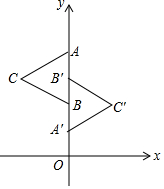
如图，正三角形ABC与正三角形A′B′C′关于某点成中心对称，已知A、B′、B三点的坐标分别是（0，4）、（0，3）、（0，2）．
太阳能光伏发电是一种清洁、安全、便利、高效的新兴能源，因而逐渐被推广使用．如图是太阳能电池板支撑架的截面图，其中的粗线表示支撑角钢，太阳能电池板与支撑角钢AB的长度相同，支撑角钢EF长为$\frac{{290\sqrt{3}}}{3}$cm，AB的倾斜角为30°，BE=CA=50cm，支撑角钢CD，EF与底座地基台面接触点分别为D，F，CD垂直于地面，FE⊥AB于点E．两个底座地基高度相同（即点D，F到地面的垂直距离相同），均为 30cm，点A到地面的垂直距离为50cm，则支撑角钢CD的长度是45cm，AB的长度是300cm．