题目内容
已知⊙O的半径为5cm，点A为线段OP的中点，当OP=6cm时，点A和⊙O的位置关系是 ．
考点：点与圆的位置关系
专题：
分析：先计算出OA的长，然后与半径比较大小，再利用点与圆的位置关系进行判断．
解答：解：点A为线段OP的中点，而OP=6cm，
所以OA=3cm，
而⊙O的半径为5cm，
所以点A在⊙O内．
故答案为点A在⊙O内．
所以OA=3cm，
而⊙O的半径为5cm，
所以点A在⊙O内．
故答案为点A在⊙O内．
点评：本题考查了点与圆的位置关系：设⊙O的半径为r，点P到圆心的距离OP=d，则有点P在圆外?d＞r；点P在圆上?d=r；点P在圆内?d＜r．
练习册系列答案
名校课堂系列答案
相关题目
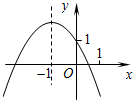已知二次函数y=ax2+bx+c的图象如图所示，有以下结论．其中，错误的结论是（ ）| A、abc＞0 | ||
| B、a+b＜-1 | ||
C、2a-b＜-
| ||
| D、c-a＞1 |
如图，如果∠3+∠4=180°，那么∠1与∠2是否相等？为什么？
如图，已知AD平分∠BAC，要使△ABD≌△ACD，下列说法正确的是（ ）
| A、方程ax2+bx+c=0是关于x的一元二次方程 |
| B、方程3x2=4的常数项是4 |
| C、当一次项系数为0时，一元二次方程总有非零解 |
| D、若一元二次方程的常数项为0，则0必是它的一个根 |
如图，在△ABC中∠C=90°，则x=计算-1
×(
+1
-
) 的结果是（ ）
| 1 |
| 7 |
| 7 |
| 8 |
| 3 |
| 4 |
| 7 |
| 12 |
A、-
| ||
| B、0 | ||
| C、1 | ||
D、
|