题目内容
19.四边形ABCD中,∠B=∠D=90°,若DC=2cm,AB=5cm,∠A=60°.求AD、BC的长.分析 首先延长AD,BC交于点E,进而利用含30度角的直角三角形的性质和勾股定理得出EC,DE的长,再利用利用含30度角的直角三角形的性质和勾股定理得出AE,BE的长,再根据线段之间的和差关系得出AD、BC的长.
解答 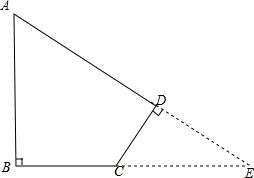 解:如图所示:延长AD,BC交于点E,
解:如图所示:延长AD,BC交于点E,
∵∠A=60°,∠B=∠D=90°,
∴∠E=30°,
∵CD=2cm,
∴EC=4cm,
∴DE=$\sqrt{C{E}^{2}-C{D}^{2}}$=2$\sqrt{3}$cm,
∵AB=5cm,
∴AE=10cm,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=5$\sqrt{3}$cm,
则AD=(10-2$\sqrt{3}$)cm,
BC=(5$\sqrt{3}$-4)cm.
点评 此题主要考查了勾股定理以及锐角三角函数关系的应用,正确得出DE,EC,AE,BE的长是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.如图所示,∠1和∠2是对顶角的是( )
| A. |  | B. | 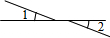 | C. | 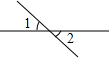 | D. | 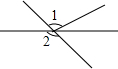 |
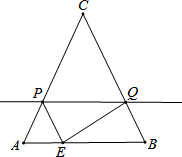 已知,如图在△ABC中,AC=BC=10,cos∠CAB=$\frac{3}{5}$与AB重合的直线PQ沿AC方向以1单位/s的速度平移,点E从点A出发沿AB方向以$\frac{6}{5}$单位/s的速度移动,当点E到达B点时,E与PQ同时停止运动.
已知,如图在△ABC中,AC=BC=10,cos∠CAB=$\frac{3}{5}$与AB重合的直线PQ沿AC方向以1单位/s的速度平移,点E从点A出发沿AB方向以$\frac{6}{5}$单位/s的速度移动,当点E到达B点时,E与PQ同时停止运动.
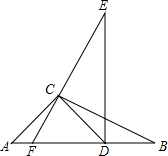 如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$.
如图,在△ABC中,AC=3$\sqrt{2}$,将△ABC绕点C逆时针转至△DEC的位置,其中点A与点D是对应点,且点D在AB边上,此时BD=3$\sqrt{3}$-3,∠BCD=15°,延长EC交AB于点F.若∠E=30°,则FD=3+$\sqrt{3}$.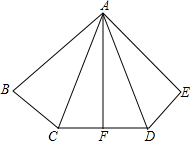 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD的中点.