题目内容
经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，如果这三种情况是等可能的，当三辆汽车经过这个十字路口时：
(1)求三辆车全部同向而行的概率；
(2)求至少有两辆车向左转的概率．
（1）（2） 【解析】试题分析：因为此题需要三步完成，所以画出树状图求解即可，注意要做到不重不漏． 试题解析：(1)画树状图如下： 总共有27种结果，每种结果出现的可能性相同．其中，三辆车全部同向而行的结果有3种，(7分)∴P(三辆车全部同向而行)＝； (2)由(1)中树状图可知至少有两辆车向左转的结果有7种， ∴P(至少有两辆车向左转)＝.
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
王老师将1个黑球和若干个白球(这些球除颜色外都相同)放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出1个球(有放回)，下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸出黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.207 | 0.30 | 0.26 | 0.254 | 0.251 |
(1)根据上表数据估计从袋中摸出1个球是黑球的概率是_________；
(2)估计袋中白球的个数．
(1)0.25(2)估计袋中有3个白球 【解析】试题分析：（1）用大量重复试验中事件发生的频率稳定到某个常数来表示该事件发生的概率即可； （2）列用概率公式列出方程求解即可； 试题解析：（1）251÷1000=0.251； ∵大量重复试验事件发生的频率逐渐稳定到0.25附近， ∴估计从袋中摸出一个球是黑球的概率是0.25； （2）设袋中白球为x个， =0....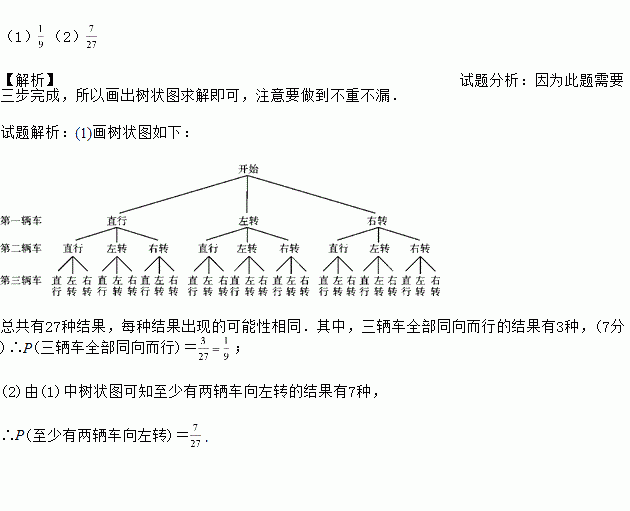
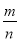
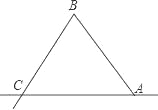
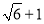的值 （ ）